
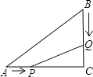
【题目】如图,△ABC中,∠C=90,AB=10cm,AC=8cm,点P从点A开始出发向点C以2cm/s的速度移动,点Q从B点出发向点C以1cm/s的速度移动,若P、Q分别同时从A,B出发,几秒后四边形APQB是△ABC面积的![]()
科目:初中数学 来源: 题型:
【题目】如图,学校准备在教学楼后面搭建一个简易矩形自行车车棚,一边利用教学楼的后墙(可利用的墙长为19 m),另外三边利用学校现有总长38 m的铁栏围成.
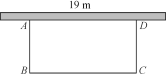
(1)若围成的面积为180 m2,试求出自行车车棚的长和宽;
(2)能围成面积为200 m2的自行车车棚吗?如果能,请你给出设计方,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料
我们通过下列步骤估计方程2x2+x﹣2=0的根的所在的范围.
第一步:画出函数y=2x2+x﹣2的图象,发现图象是一条连续不断的曲线,且与x轴的一个
交点的横坐标在0,1之间.
第二步:因为当x=0时,y=﹣2<0;当x=1时,y=1>0.
所以可确定方程2x2+x﹣2=0的一个根x1所在的范围是0<x1<1.
第三步:通过取0和1的平均数缩小x1所在的范围;
取x=![]() ,因为当x=
,因为当x=![]() 时,y<0,
时,y<0,
又因为当x=1时,y>0,
所以![]() <x1<1.
<x1<1.
(1)请仿照第二步,通过运算,验证2x2+x﹣2=0的另一个根x2所在范围是﹣2<x2<﹣1;
(2)在﹣2<x2<﹣1的基础上,重复应用第三步中取平均数的方法,将x2所在范围缩小至m<x2<n,使得n﹣m≤![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=ax2+bx+c(a≠0)的图象于x轴的交点坐标分别为(x1,0),(x2,0),且x1<x2,图象上有一点M(x0,y0)在x轴下方,对于以下说法:①b2﹣4ac>0②x=x0是方程ax2+bx+c=y0的解③x1<x0<x2④a(x0﹣x1)(x0﹣x2)<0其中正确的是( )
A.①③④B.①②④C.①②③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区决定把一块长![]() ,宽
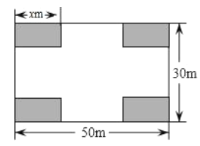
,宽![]() 的矩形空地建成居民健身广场,设计方案如图,阴影区域为绿化区(四块绿化区为大小、形状都相同的矩形),空白区域为活动区,且四周的4个出口宽度相同,其宽度不小于
的矩形空地建成居民健身广场,设计方案如图,阴影区域为绿化区(四块绿化区为大小、形状都相同的矩形),空白区域为活动区,且四周的4个出口宽度相同,其宽度不小于![]() ,不大于
,不大于![]() ,设绿化区较长边为
,设绿化区较长边为![]() ,活动区的面积为
,活动区的面积为![]() .为了想知道出口宽度的取值范围,小明同学根据出口宽度不小于
.为了想知道出口宽度的取值范围,小明同学根据出口宽度不小于![]() ,算出
,算出![]() .
.
(1)求![]() 与
与![]() 的函数关系式并直接写出自变量
的函数关系式并直接写出自变量![]() 的取值范围;
的取值范围;
(2)求活动区的最大面积;
(3)预计活动区造价为50元/![]() ,绿化区造价为40元/
,绿化区造价为40元/![]() ,若社区的此项建造投资费用不得超过72000元,求投资费用最少时活动区的出口宽度?
,若社区的此项建造投资费用不得超过72000元,求投资费用最少时活动区的出口宽度?
查看答案和解析>>
科目:初中数学 来源: 题型:
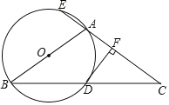
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
(1)试说明DF是⊙O的切线;
(2)若AC=3AE=6,求tanC
查看答案和解析>>
科目:初中数学 来源: 题型:
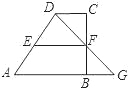
【题目】如图,梯形ABCD中,AB∥CD,点F在BC上,连DF与AB的延长线交于点G.
(1)求证:△CDF∽△BGF;
(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=6cm,EF=4cm,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要证明平行四边形ABCD为正方形,那么我们需要在四边形ABCD是平行四边形的基础上,进一步证明( )
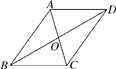
A.AB=AD且AC⊥BDB.AB=AD且AC=BDC.∠A=∠B且AC=BDD.AC和BD互相垂直平分
查看答案和解析>>
科目:初中数学 来源: 题型:
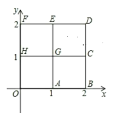
【题目】如图,2×2网格(每个小正方形的边长为1)中有A,B,C,D,E,F,G,H,O九个格点.抛物线l的解析式为![]() (n为整数).若l经过这九个格点中的三个,则满足这样条件的抛物线条数为_________条
(n为整数).若l经过这九个格点中的三个,则满足这样条件的抛物线条数为_________条
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com