
����Ŀ��С����С����һ������ɫ������Ϸ����ͼ��������������ת����ת�̣�ÿ��ת�̱��ֳ������ȵļ������Σ���Ϳ��ͼ����ʾ����ɫ��ͬʱת������ת�̣����ת��Aת���˺�ɫ��ת��Bת������ɫ������ת��Aת������ɫ��ת��Bת���˺�ɫ�����ɫ����ɫ��һ�������ɫ�����������С����ʤ��ͬ������ɫ�ͻ�ɫ��һ�������ɫ�����������С����ʤ������������£���С����С������ʤ����
��1�������б�����״ͼ�ķ�����ʾ����Ϸ���п��ܳ��ֵĽ����
��2������Ϸ�Ĺ���С����С����ƽ����˵�����ɣ�

���𰸡�(1)���п��ܵĽ������������2������ƽ.
��������
���⣨1���������⣬���б��������п��ܳ��ֵĽ�������ɵô𰸣�
��2���ɣ�1���ı��������ܵõ���ɫ����ɫ�ĸ��ʣ��õ����۲���ƽ��
�����������1�����б��������п��ܳ��ֵĽ����ʾ���£����п��ܳ��ֵĽ������12�֣�
�� | ���죬�죩 | �������죩 | ���ƣ��죩 |
�� | ���죬���� | ���������� | ���ƣ����� |
�� | ���죬�죩 | �������죩 | ���ƣ��죩 |
�� | ���죬�ƣ� | �������ƣ� | ���ƣ��ƣ� |
�� | �� | �� |
��2������ƽ��
����ȿ��ܳ��ֵ�12�ֽ���У���3��������ܵõ���ɫ���������ɫ�ĸ�����![]() ����С����ʤ�ĸ�����
����С����ʤ�ĸ�����![]() ����ֻ��2������ſ��ܵõ���ɫ�������ɫ�ĸ�����
����ֻ��2������ſ��ܵõ���ɫ�������ɫ�ĸ�����![]() ����Сǿ��ʤ�ĸ�����
����Сǿ��ʤ�ĸ�����![]() ����
����![]() ��
��![]() ����С����ʤ�Ŀ����Դ��������ɫ����Ϸ��˫���Dz���ƽ�ģ�
����С����ʤ�Ŀ����Դ��������ɫ����Ϸ��˫���Dz���ƽ�ģ�


 �����ÿ�ʱѵ��ϵ�д�
�����ÿ�ʱѵ��ϵ�д� ��Ԫȫ��������ϵ�д�
��Ԫȫ��������ϵ�д� �»ƸԱ����ܾ�ϵ�д�
�»ƸԱ����ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�е�ͼ��M��N���������¶��壺PΪͼ��M������һ�㣬QΪͼ��N������һ�㣬���P��Q�����ľ�������Сֵ����ô�������СֵΪͼ��M��N��ġ����롱������![]() �ر�أ���ͼ��M��N�й����㣬�涨
�ر�أ���ͼ��M��N�й����㣬�涨![]() ��
��
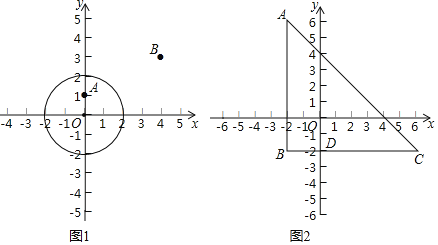
![]() ��ͼ1��
��ͼ1��![]() �İ뾶Ϊ2��
�İ뾶Ϊ2��
![]() ��
��![]() ��
��![]() ����
����![]() ______��
______��![]() ______��
______��
![]() ��ֱ֪��l��
��ֱ֪��l��![]() ��
��![]() �ġ����롱
�ġ����롱![]() ����b��ֵ��
����b��ֵ��
![]() ��֪��
��֪��![]() ��
��![]() ��
��![]() ��Բ��Ϊ
��Բ��Ϊ![]() ���뾶Ϊ
���뾶Ϊ![]() ��
��![]() ����ֱ��д��m��ȡֵ��Χ______��
����ֱ��д��m��ȡֵ��Χ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB��AC����PΪ��ABC��һ�㣬��APB����BAC��120������AP��BP��4����PC����СֵΪ�� ��
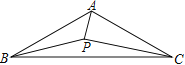
A. 2B. ![]() C.
C. ![]() D. 3
D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
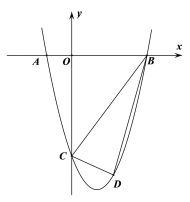
����Ŀ����ͼ����ƽ��ֱ������ϵ��������![]() ��x���ڵ�A��B����y���ڵ�C�� A��B���������Ϊ-1��3��C��������Ϊ-4.
��x���ڵ�A��B����y���ڵ�C�� A��B���������Ϊ-1��3��C��������Ϊ-4.
��1���������ߵĽ���ʽ��
��2������D�ڵ������������������ϣ�����BCD������ʱ����D�����꣬�����BCD��������ֵ��
��3�������ߵĶԳ������Ƿ����һ��Q��ʹ�á�QBC=45�㣬������ڣ������Q�����꣬������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в���
����ͨ�����в�����Ʒ���2x2+x��2=0�ĸ������ڵķ�Χ��
��һ������������y=2x2+x��2��ͼ����ͼ����һ���������ϵ����ߣ�����x���һ��
����ĺ�������0��1֮�䣮
�ڶ�������Ϊ��x=0ʱ��y=��2��0����x=1ʱ��y=1��0��
���Կ�ȷ������2x2+x��2=0��һ����x1���ڵķ�Χ��0��x1��1��
��������ͨ��ȡ0��1��ƽ������Сx1���ڵķ�Χ��
ȡx=![]() ����Ϊ��x=
����Ϊ��x=![]() ʱ��y��0��
ʱ��y��0��
����Ϊ��x=1ʱ��y��0��
����![]() ��x1��1��
��x1��1��
��1������յڶ�����ͨ�����㣬��֤2x2+x��2=0����һ����x2���ڷ�Χ�ǩ�2��x2����1��
��2���ک�2��x2����1�Ļ����ϣ��ظ�Ӧ�õ�������ȡƽ�����ķ�������x2���ڷ�Χ��С��m��x2��n��ʹ��n��m��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�����ȡ���꼶����ͬѧ����һ������Ϊ�����ʺ��Լ��Ŀ�ǰ��ѹ��ʽ���ĵ�����ѧУ�ռ��������ݺ���ѹ��ʽ��Ϊ���࣬��������ͼ1��ͼ2������������ͳ��ͼ�������ͼ�е���Ϣ����������⣺
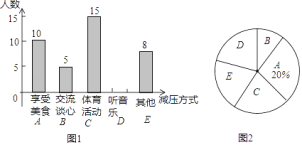
![]() ���꼶���ܵ����ͬѧ���ж�����������ȫ����ͳ��ͼ��
���꼶���ܵ����ͬѧ���ж�����������ȫ����ͳ��ͼ��
![]() ���꼶����500��ѧ����������Ƹ�У���꼶�����ּ�ѹ��ѧ���ж�������
���꼶����500��ѧ����������Ƹ�У���꼶�����ּ�ѹ��ѧ���ж�������
![]() ��ϲ��������̸������5��ͬѧ������������������Ů����������ʦ���5��ͬѧ����ѡ����ͬѧ���н��������û���״ͼ���б��ķ�����ͬʱѡ��������ͬѧ����Ů���ĸ��ʣ�
��ϲ��������̸������5��ͬѧ������������������Ů����������ʦ���5��ͬѧ����ѡ����ͬѧ���н��������û���״ͼ���б��ķ�����ͬʱѡ��������ͬѧ����Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������κ���y��ax2+bx+c��a��0����ͼ����x��Ľ�������ֱ�Ϊ��x1��0������x2��0������x1��x2��ͼ������һ��M��x0��y0����x���·�����������˵������b2��4ac��0��x��x0�Ƿ���ax2+bx+c��y0�Ľ��x1��x0��x2��a��x0��x1����x0��x2����0������ȷ���ǣ�������
A.�٢ۢ�B.�٢ڢ�C.�٢ڢ�D.�ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC����ABΪֱ���ġ�O��BC�ཻ�ڵ�D����CA���ӳ����ཻ�ڵ�E������D��DF��AC�ڵ�F.
(1)��˵��DF�ǡ�O�����ߣ�
(2)��AC=3AE=6����tanC
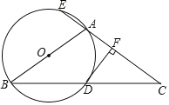
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�������һ�����⣺����![]() ��һԪ���η���
��һԪ���η���![]() ����������ȵ��ҷ����ʵ����̽��
����������ȵ��ҷ����ʵ����̽��![]() ��
��![]() ��
��![]() ���������.
���������.
С������ѧϰ�����ľ��飬��Ϊ���ԴӶ��κ����ĽǶȿ�һԪ���η��̣�������С����̽�����̣�����һԪ���η���![]() ��Ӧ�Ķ��κ���Ϊ
��Ӧ�Ķ��κ���Ϊ![]() ��
��
�ڽ������κ���ͼ���Եõ���Ӧ��һԪ������![]() ��
��![]() ��
��![]() ������������б����£�
������������б����£�
���̸��ļ������壺
������������� | ��Ӧ�Ķ��κ����Ĵ���ͼ�� |
|
��������������ȵĸ�ʵ�� |
|
|
____________ |
|
|
��������������ȵ���ʵ�� | ____________ | ____________ |
��1���ο�С��������������������������
��2����һԪ���η���![]() ��һ����ʵ����һ����ʵ�����Ҹ�ʵ������-1����ʵ��
��һ����ʵ����һ����ʵ�����Ҹ�ʵ������-1����ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com