
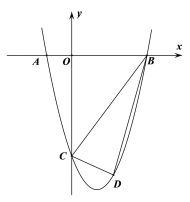
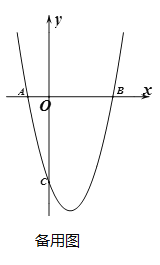
【题目】如图,在平面直角坐标系中抛物线![]() 交x轴于点A、B,交y轴于点C, A、B两点横坐标为-1和3,C点纵坐标为-4.
交x轴于点A、B,交y轴于点C, A、B两点横坐标为-1和3,C点纵坐标为-4.
(1)求抛物线的解析式;
(2)动点D在第四象限且在抛物线上,当△BCD面积最大时,求D点坐标,并求△BCD面积的最大值;
(3)抛物线的对称轴上是否存在一点Q,使得∠QBC=45°,如果存在,求出点Q的坐标,不存在说明理由.
【答案】(1) ;(2)D(
;(2)D(![]() ,-5),最大值
,-5),最大值![]() ;(3)(1,
;(3)(1,![]() ).
).
【解析】
(1)将A,B,C三点坐标代入抛物线![]() ,即可求出;
,即可求出;
(2)作DH垂直AB于H,设D点坐标为(x,y),则有OC=4,OB=3,OH=x,HD=-y,由 ![]() ,
, ,化简即可出;
,化简即可出;
(3)由函数关系式: 化简得对称轴为
化简得对称轴为![]() ,作出对称轴
,作出对称轴![]() ,交x轴于F点,连接CB,交对称轴于E点,求出BC的函数解析式,则可以知道E点坐标为:(1,
,交x轴于F点,连接CB,交对称轴于E点,求出BC的函数解析式,则可以知道E点坐标为:(1,![]() ),所以存在一点Q,使得∠QBC=45°,并且点Q在FE之间,设Q点坐标为:(1,
),所以存在一点Q,使得∠QBC=45°,并且点Q在FE之间,设Q点坐标为:(1,![]() ),求出线段
),求出线段![]() 的斜率
的斜率![]() ,线段
,线段![]() 的斜率
的斜率![]() ,利用两直线相交交角为
,利用两直线相交交角为![]() ,得到
,得到![]() ,化简即可。
,化简即可。
解:(1)由图像可知:A,B,C,三点的坐标分别是(-1,0),(3,0),(0,-4),
将A,B,C三点坐标代入抛物线![]()
得: ,解之得:
,解之得:
∴抛物线的解析式为: ;
;
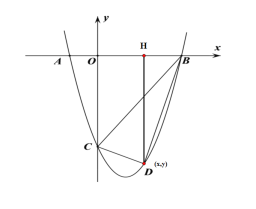
(2)如图,作DH垂直AB于H,设D点坐标为(x,y),
则有:OC=4,OB=3,OH=x,HD=-y,HB=3-x,
∴梯形CDHO为直角梯形,
∴![]()
即:![]()
![]()
![]()
又∵D点在抛物线 上,
上,
∴![]()
![]()
![]()
∴当![]() 时,△BCD面积有最大值,是
时,△BCD面积有最大值,是![]() ,
,
∴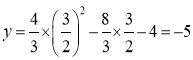
所以D点坐标为:(![]() ,-5);
,-5);
(3)由函数关系式: 化简得:
化简得: ,
,
∴对称轴为:![]() ,
,
如图示:作出对称轴![]() ,交x轴于F点,连接CB,交对称轴于E点,
,交x轴于F点,连接CB,交对称轴于E点,

∴由B,C,的坐标分别是(3,0),(0,-4),设BC的函数解析式为:![]()
则:![]() ,解之得:
,解之得:
∴BC的函数解析式为:![]() ,当
,当![]() 时,
时,![]() ,
,
∴E点坐标为:(1,![]() ),
),
∴BF=2,FE=![]() ,
,
∴ ,
,
即:![]()
∴存在一点Q,使得∠QBC=45°,并且点Q在FE之间,
设Q点坐标为:(1,![]() )
)
∴![]() ,
,![]() ,
,
∵直线BQ和BC的交角为![]() ,
,
∴![]()
即:
化简得:![]() ,
,
∴Q点坐标为:(1,![]() )
)


科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() 在以
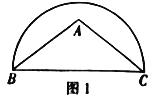
在以![]() 为直径的半圆内.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).
为直径的半圆内.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).
(1)在图1中作弦![]() ,使
,使![]() ;
;
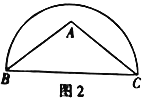
(2)在图2中以![]() 为边作一个45°的圆周角.
为边作一个45°的圆周角.
查看答案和解析>>
科目:初中数学 来源: 题型:
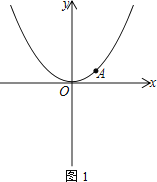
【题目】已知抛物线y=ax2经过点A(2,1).
(1) 求a的值;
(2) 如图1,点M为x轴负半轴上一点,线段AM交抛物线于N.若△OMN为等腰三角形,求点N的坐标;
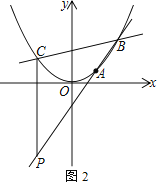
(3) 如图2,直线y=kx-2k+3交抛物线于B、C两点,过点C作CP⊥x轴,交直线AB于点P,请说明点P一定在某条确定的直线上运动,求出这条直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
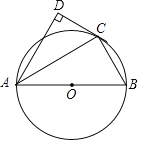
【题目】如图,AB为⊙O的直径,点D在⊙O外,∠BAD的平分线与⊙O交于点C,连接BC、CD,且∠D=90°.
(1)求证:CD是⊙O的切线;
(2)若∠DCA=60°,BC=3,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝新中国成立70周年,并体现绿色节能理念,我市某工厂降低了某种工艺品的成本,两个月内从每件产品成本50元,降低到了每件32元,
(1)请问工厂平均每月降低率为多少?
(2)该工厂将产品投放市场进行实销,经过调查,得到如下数据:
销售单价 | …… | 40 | 50 | 60 | 70 | …… |
每天销售量 | …… | 400 | 300 | 200 | 100 | …… |
把上表中![]() 、
、![]() 的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想
的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想![]() 与
与![]() 的函数关系,并求出函数关系式.
的函数关系,并求出函数关系式.
(3)当销售单价定为多少时,工艺厂试销该工艺品每天活得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小芳做一个“配色”的游戏.右图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并涂上图中所示的颜色.同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,或者转盘A转出了蓝色,转盘B转出了红色,则红色和蓝色在一起配成紫色,这种情况下小芳获胜;同样,蓝色和黄色在一起配成绿色,这种情况下小明获胜;在其它情况下,则小明、小芳不分胜负.
(1)利用列表或树状图的方法表示此游戏所有可能出现的结果;
(2)此游戏的规则,对小明、小芳公平吗?试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新定义:[a,b,c]为二次函数y=ax2+bx+e(a≠0,a,b,c为实数)的“图象数”,如:y=-x2+2x+3的“图象数”为[-1,2,3]
(1)二次函数y=![]() x2-x-1的“图象数”为 .
x2-x-1的“图象数”为 .
(2)若图象数”是[m,m+1,m+1]的二次函数的图象与x轴只有一个交点,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(m-1)x2-x-2=0.
(1)当m为何实数时,方程有两个不相等的实数根?
(2)若x1,x2是方程的两个根,且x![]() x2+x1x
x2+x1x![]() =-
=-![]() ,试求实数m的值.
,试求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com