【题目】解方程：
（1）（x+2）2＝25
（2）x2﹣2x﹣2＝0
（3）x2﹣6x﹣16＝0
（4）（x﹣2）2﹣（3x+8）2＝0
【答案】（1）x＝3或x＝﹣7；（2）x＝1+
或x＝1﹣；（3）x＝﹣2或x＝8；（4）x＝﹣
或x＝﹣5
【解析】
（1）运用直接开平方法解答即可;(2)运用配方法解答即可;(3) (4)运用分解因式法即可.
解：（1）（x+2）2＝25
∴x+2＝5或x+2＝﹣5，
解得：x＝3或x＝﹣7；
（2）x2﹣2x﹣2＝0，
x2﹣2x＝2，
x2﹣2x+1＝2+1，即（x﹣1）2＝3，
∴x﹣1＝或x﹣1＝﹣，
解得：x＝1+或x＝1﹣；
（3）x2﹣6x﹣16＝0
（x+2）（x﹣8）＝0，
∴x+2＝0或x﹣8＝0，
解得：x＝﹣2或x＝8；
（4）（x﹣2）2﹣（3x+8）2＝0
因式分解可得：（x﹣2+3x+8）（x﹣2﹣3x﹣8）＝0，
即（4x+6）（﹣2x﹣10）＝0，
∴4x+6＝0或﹣2x﹣10＝0，
解得：x＝﹣或x＝﹣5．
科目：初中数学 来源： 题型：
【题目】在甲、乙两名同学中选拔一人参加“英语口语听力”大赛，在相同的测试条件下，两人5次测试成绩（单位：分）如下：
甲：79，81，82，85，83 乙：88，79，90，81，72．
（1）求甲、乙两名同学测试成绩的方差；
（2）请你选择一个角度来判断选拔谁参加比赛更合适．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中的图形M，N，给出如下定义：P为图形M上任意一点，Q为图形N上任意一点，如果P，Q两点间的距离有最小值，那么称这个最小值为图形M，N间的“距离”，记作
特别地，若图形M，N有公共点，规定
．
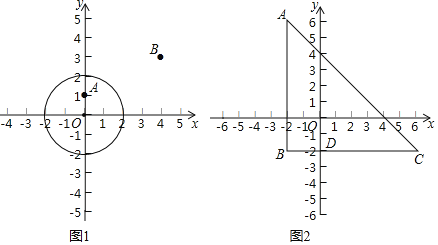
如图1，
的半径为2，
点
，
，则
______，
______．
已知直线l：
与的“距离”
，求b的值．
已知点
，
，
的圆心为
，半径为
若
，请直接写出m的取值范围______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC.（1）请用圆规和直尺作出⊙P，使圆心P到AB边和BC边的距离相等，且⊙P经过A，B两点（保留作图痕迹，不写作法和证明）；
（2）若∠B=60°，AB=6，求⊙P的半径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，学校准备在教学楼后面搭建一个简易矩形自行车车棚，一边利用教学楼的后墙(可利用的墙长为19 m)，另外三边利用学校现有总长38 m的铁栏围成．
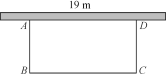
(1)若围成的面积为180 m2，试求出自行车车棚的长和宽；
(2)能围成面积为200 m2的自行车车棚吗？如果能，请你给出设计方,如果不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
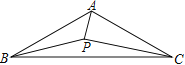
【题目】如图，△ABC中，AB＝AC，点P为△ABC内一点，∠APB＝∠BAC＝120°．若AP＋BP＝4，则PC的最小值为（ ）
A. 2B. 
C. 
D. 3
查看答案和解析>>
科目：初中数学 来源： 题型：
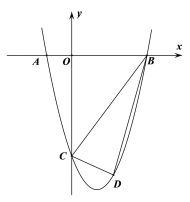
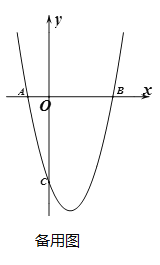
【题目】如图，在平面直角坐标系中抛物线
交x轴于点A、B，交y轴于点C， A、B两点横坐标为-1和3，C点纵坐标为-4.
（1）求抛物线的解析式；
（2）动点D在第四象限且在抛物线上，当△BCD面积最大时，求D点坐标，并求△BCD面积的最大值；
（3）抛物线的对称轴上是否存在一点Q，使得∠QBC=45°，如果存在，求出点Q的坐标，不存在说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
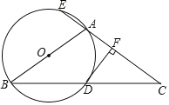
【题目】如图，△ABC中，AB=AC，以AB为直径的⊙O与BC相交于点D，与CA的延长线相交于点E，过点D作DF⊥AC于点F.
(1)试说明DF是⊙O的切线；
(2)若AC=3AE=6，求tanC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
