
【题目】在![]() 中,
中,![]() ,点
,点![]() 在以
在以![]() 为直径的半圆内.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).
为直径的半圆内.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).
(1)在图1中作弦![]() ,使
,使![]() ;
;
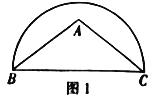
(2)在图2中以![]() 为边作一个45°的圆周角.
为边作一个45°的圆周角.
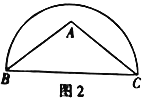
【答案】(1)见解析;(2)见解析
【解析】
(1)分别延长![]() 、
、![]() 交半圆于
交半圆于![]() 、
、![]() ,利用圆周角定理可等腰三角形的性质可得到
,利用圆周角定理可等腰三角形的性质可得到![]() ,则可判断
,则可判断![]() ;
;
(2)在(1)基础上分别延长![]() 、
、![]() ,它们相交于
,它们相交于![]() ,则连接
,则连接![]() 交半圆于
交半圆于![]() ,然后证明
,然后证明![]() ,从而根据圆周角定理可判断
,从而根据圆周角定理可判断![]() .
.
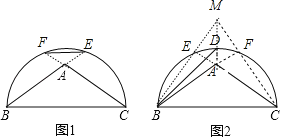
解:(1)如下图:分别延长![]() 、
、![]() 交半圆于
交半圆于![]() 、
、![]() ,线段
,线段![]() 为所求弦.
为所求弦.
理由如下:∵AB=BC,
∴∠B=∠C,
又∵![]() ,
,
∴∠F=∠C,
∴∠C=∠F,
∴EF∥BC,
(2)如下图,(以下画法供参考):在(1)基础上分别延长![]() 、
、![]() ,它们相交于
,它们相交于![]() ,则连接
,则连接![]() 交半圆于
交半圆于![]() , 则
, 则![]() 为所作.
为所作.
理由如下:∵EF∥BC,
∴![]() ,
,
∴∠EBC=∠FCB,
∴MC=MB,
又∵AB=AC,
∴MA垂直平分BC,
∴D为![]() 的中点,
的中点,
∵![]() 为半圆,
为半圆,
∴∠CBD=45°.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】在直角坐标系中,已知直线![]() 分别于
分别于![]() 轴和
轴和![]() 轴交于
轴交于![]() ,
,![]() 两点,将抛物线
两点,将抛物线![]() 平移,得到抛物线
平移,得到抛物线![]() ,使抛物线
,使抛物线![]() 过点
过点![]() ,
,![]() 两点.
两点.
①求交点![]() ,
,![]() 的坐标;
的坐标;
②求抛物线![]() 的函数表达式;
的函数表达式;
③求抛物线的顶点坐标和对称轴方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两名同学中选拔一人参加“英语口语听力”大赛,在相同的测试条件下,两人5次测试成绩(单位:分)如下:
甲:79,81,82,85,83 乙:88,79,90,81,72.
(1)求甲、乙两名同学测试成绩的方差;
(2)请你选择一个角度来判断选拔谁参加比赛更合适.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=ax2+bx+3经过点A(3,0)和点B(4,3).
(1)求这条抛物线的函数表达式;
(2)求该抛物线的顶点坐标;
(3)在给定坐标系内画出这条抛物线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:
(1)用开平方法解方程:![]()
(2)用配方法解方程:x2 —4x+1=0
(3)用公式法解方程:3x2+5(2x+1)=0
(4)用因式分解法解方程:3(x-5)2=2(5-x)
(5)解方程:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
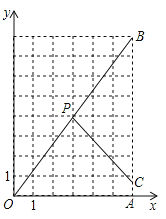
【题目】已知:Rt△OAB在直角坐标系中的位置如图所示,P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分。
问:点C在什么位置时,分割得到的三角形与Rt△OAB相似(注:在图上画出所有符合要求的线段PC,并求出相应的点C的坐标).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中的图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最小值,那么称这个最小值为图形M,N间的“距离”,记作![]() 特别地,若图形M,N有公共点,规定
特别地,若图形M,N有公共点,规定![]() .
.
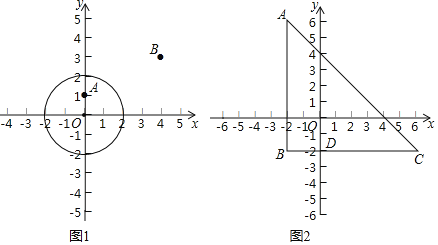
![]() 如图1,
如图1,![]() 的半径为2,
的半径为2,
![]() 点
点![]() ,
,![]() ,则
,则![]() ______,
______,![]() ______.
______.
![]() 已知直线l:
已知直线l:![]() 与
与![]() 的“距离”
的“距离”![]() ,求b的值.
,求b的值.
![]() 已知点
已知点![]() ,
,![]() ,
,![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() 若
若![]() ,请直接写出m的取值范围______.
,请直接写出m的取值范围______.
查看答案和解析>>
科目:初中数学 来源: 题型:
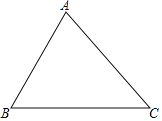
【题目】如图,已知△ABC.(1)请用圆规和直尺作出⊙P,使圆心P到AB边和BC边的距离相等,且⊙P经过A,B两点(保留作图痕迹,不写作法和证明);
(2)若∠B=60°,AB=6,求⊙P的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
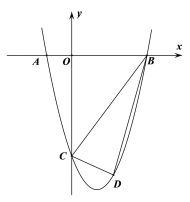
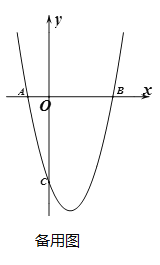
【题目】如图,在平面直角坐标系中抛物线![]() 交x轴于点A、B,交y轴于点C, A、B两点横坐标为-1和3,C点纵坐标为-4.
交x轴于点A、B,交y轴于点C, A、B两点横坐标为-1和3,C点纵坐标为-4.
(1)求抛物线的解析式;
(2)动点D在第四象限且在抛物线上,当△BCD面积最大时,求D点坐标,并求△BCD面积的最大值;
(3)抛物线的对称轴上是否存在一点Q,使得∠QBC=45°,如果存在,求出点Q的坐标,不存在说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com