
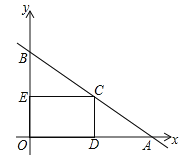
【题目】在平面直角坐标系中,直线AB与x轴、y轴分别交于A(6,0),B(0,3)两点.点C为线段AB上的一个动点,过点C作CD⊥x轴于点D,作CE⊥y轴与点E,求矩形OECD的最大面积,并求此时点C的坐标.
 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
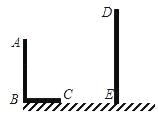
【题目】如图,AB和DE是直立在地面上的两根立柱.AB=5m,某一时刻AB在阳光下的投影BC=3m,同时测量出DE在阳光下的投影长为6m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)请你计算DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
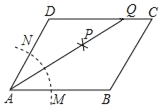
【题目】如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于![]() MN长为半径作弧,两弧相交于点P;③作射线AP,交边CD于点Q,若DC=3QC,BC=6,则平行四边形ABCD周长为_____.
MN长为半径作弧,两弧相交于点P;③作射线AP,交边CD于点Q,若DC=3QC,BC=6,则平行四边形ABCD周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生的身体素质,教育行政部门规定学生每天户外活动的平均时间不少于1小时,为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制成如图中两幅不完整的统计,请你根据图中提供的信息解答下列问题:


(1)在这次调查中共调查了多少名学生?
(2)求7户外活动时间为0.5小时的人数,并补充频数分布直方图;
(3)求表示户外活动时间为2小时的扇形圆心角的度数;
(4)本次调查中学生参加户外活动的平均时间是否符合要求?户外活动时间的众数和中位数各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅用一块长为12分米,宽为8分米的矩形铁皮制作一个无盖长方体容器,需要将四角各裁掉一个正方形.(厚度不计)
(1)请在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求当长方体底面面积为32平方分米时,裁掉的正方形边长是多少?
(2)若要求制作的长方体的底面长不大于底面宽的5倍(长大于宽),并将容器外表面进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,求裁掉的正方形边长为多少时,总费用最低,最低费用为多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2﹣2ax﹣3a(a<0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴的正半轴交于点C,顶点为D.
(1)求顶点D的坐标(用含a的代数式表示);
(2)若以AD为直径的圆经过点C.
①求抛物线的函数关系式;
②如图2,点E是y轴负半轴上一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段MF:BF=1:2,求点M、N的坐标;
③点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,如图3,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以直线x=1为对称轴的抛物线y=-x2+bx+c与x轴交于A、B两点,其中点A的坐标为(3,0).
(1)求点B的坐标;
(2)设点M(x1,y1)、N(x2,y2)在抛物线线上,且x1<x2<1,试比较y1、y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
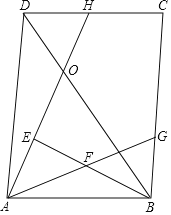
【题目】如图,在平行四边形ABCD中,点H为DC上一点,BD、AH交于点O,△ABO为等边三角形,点E在线段AO上,OD=OE,连接BE,点F为BE的中点,连接AF并延长交BC于点G,且∠GAD=60°.
(1)若CH=2,AB=4,求BC的长;
(2)求证:BD=AB+AE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com