
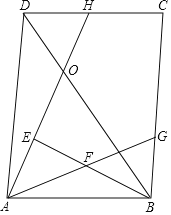
【题目】如图,在平行四边形ABCD中,点H为DC上一点,BD、AH交于点O,△ABO为等边三角形,点E在线段AO上,OD=OE,连接BE,点F为BE的中点,连接AF并延长交BC于点G,且∠GAD=60°.
(1)若CH=2,AB=4,求BC的长;
(2)求证:BD=AB+AE.
【答案】(1)![]() ;(2)详见解析
;(2)详见解析
【解析】
(1)延长AH、BC相交于点M,可证明△MCH∽△MBA,得出MH=AH,BM=2BC;由∠DOH=∠AOB=60°,∠ODH=∠OBA=60°,∠OHD=∠OAB=60°,可得△DOH是等边三角形,AE=OA-OE=OA-OD=2,得点E是OA的中点,根据“三线合一”可得BE的长度、BE⊥OA,根据勾股定理求出BM的长,而BC=![]() BM;
BM;
(2)AB=OB,由(1)知,AE=OE=OD,可证BD=OB+OD=AB+AE.
解:延长AH、BC相交于点M,
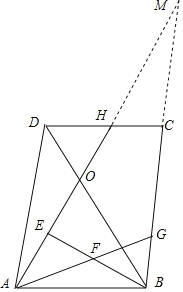
∵ABCD
∴CD=AB=4,CD∥AB
∴∠MHC=∠MAB,∠MCH=∠MBA
∴△MCH∽△MBA
![]()
∵CH=2
![]()
∴MH=AH,BM=2BC
∵△ABO为等边三角形
∴∠AOB=∠OAB=∠OBA=60°,OA=AB=4
∴∠DOH=∠AOB=60°
∴∠ODH=∠OBA=60°,∠OHD=∠OAB=60°
∴∠DOH=∠ODH=∠OHD
∴△DOH是等边三角形
∴OH=OD=DH=2
∴MH=AH=OA+OH=4+2=6,EM=OE+OH+MH=10
∵OD=OE=2
∴AE=OA﹣OE=4﹣2=2
∴点E是OA的中点
∵△ABO为等边三角形
∴BE⊥OA,∠ABE=30°
![]()
在Rt△BEM中,∠BEM=90°
∴BE2+EM2=BM2
![]()
![]()
![]()
(2)∵△ABO为等边三角形
∴AB=OB
由(1)知,AE=OE=OD
∵BD=OB+OD
∴BD=AB+AE


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
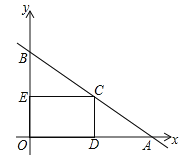
【题目】在平面直角坐标系中,直线AB与x轴、y轴分别交于A(6,0),B(0,3)两点.点C为线段AB上的一个动点,过点C作CD⊥x轴于点D,作CE⊥y轴与点E,求矩形OECD的最大面积,并求此时点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户种植花生,原来种植的花生亩产量为200千克,出油率为50%(即每100千克花生可加工成花生油50千克).现在种植新品种花生后,每亩收获的花生可加工成花生油132千克,其中花生出油率的增长率是亩产量的增长率的二分之一.则新品种花生亩产量的增长率为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(﹣2,0),与反比例函数在第一象限内的图象的交于点B(2,n),连接BO,若S△AOB=4.
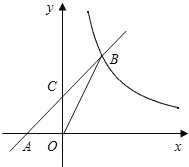
(1)求该反比例函数的解析式和直线AB的解析式;
(2)若直线AB与y轴的交点为C,求△OCB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(m+3)x+m+1=0.
(1)求证:无论m取何值,原方程总有两个不相等的实数根;
(2)若x1,x2是原方程的两根,且|x1-x2|=2![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:①抛物线过原点; ②4a+b+c=0; ③a+b>0; ④该二次函数的最小值为b;⑤当0<x<4时,y>0.正确的是( )
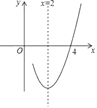
A. ①② B. ③④⑤ C. ①②④ D. ①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
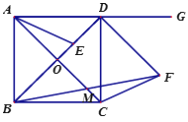
【题目】如图,已知正方形ABCD,对角线AC、BD交于点O,点E在对角线BD上,连接AE.点G是AD延长线上一点,DF平分∠GDC,且DF=BE,连接FB、FC,FB与AC交于点M.
(1)若点E是BD的三等分点(DE<BE),BF=![]() ,求△ABE的面积;
,求△ABE的面积;
(2)求证:DE=2CM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学选拔一名青年志愿者:经笔试、面试,结果小明和小丽并列第一.评委会决定通过抓球来确定人选.规则如下:在不透明的布袋里装有除颜色之外均相同的2个红球和1个绿球,小明先取出一个球,记住颜色后放回,然后小丽再取出一个球.若两次取出的球都是红球,则小明胜出;若两次取出的球是一红一绿,则小丽胜出.你认为这个规则对双方公平吗?请用列表法或画树状图的方法进行分析.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com