
【题目】某中学选拔一名青年志愿者:经笔试、面试,结果小明和小丽并列第一.评委会决定通过抓球来确定人选.规则如下:在不透明的布袋里装有除颜色之外均相同的2个红球和1个绿球,小明先取出一个球,记住颜色后放回,然后小丽再取出一个球.若两次取出的球都是红球,则小明胜出;若两次取出的球是一红一绿,则小丽胜出.你认为这个规则对双方公平吗?请用列表法或画树状图的方法进行分析.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
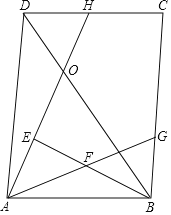
【题目】如图,在平行四边形ABCD中,点H为DC上一点,BD、AH交于点O,△ABO为等边三角形,点E在线段AO上,OD=OE,连接BE,点F为BE的中点,连接AF并延长交BC于点G,且∠GAD=60°.
(1)若CH=2,AB=4,求BC的长;
(2)求证:BD=AB+AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y (℃)与时间x(h)之间的函数关系,其中线段AB、BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)求这天的温度y与时间x(0≤x≤24)的函数关系式;
(2)求恒温系统设定的恒定温度;
(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,直线
,直线![]() 是足球场的底线,
是足球场的底线,![]() 是球门,
是球门,![]() 点是射门点,连接
点是射门点,连接![]() ,
,![]() 叫做射门角.
叫做射门角.
(1)如图![]() ,点
,点![]() 是射门点,另一射门点
是射门点,另一射门点![]() 在过
在过![]() 三点的圆外(未超过底线
三点的圆外(未超过底线![]() ).证明:
).证明:![]()
(2)如图![]() ,
,![]() 经过球门端点
经过球门端点![]() ,直线
,直线![]() ,垂足为
,垂足为![]() 且与
且与![]() 相切与点
相切与点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,求此时一球员带球沿直线
,求此时一球员带球沿直线![]() 向底线方向运球时最大射门角的度数.
向底线方向运球时最大射门角的度数.
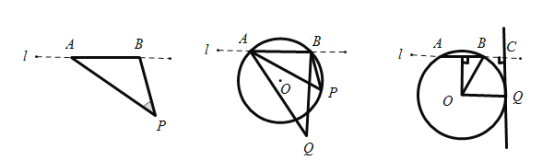
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
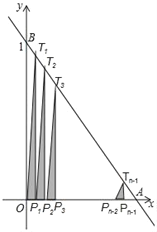
【题目】如图,直线y=﹣x+1与两坐标轴分别交于A,B两点,将线段OA分成n等份,分点分别为P1,P2,P3,…,Pn﹣1,过每个分点作x轴的垂线分别交直线AB于点T1,T2,T3,…,Tn﹣1,用S1,S2,S3,…,Sn﹣1分别表示Rt△T1OP1,Rt△T2P1P2,…,Rt△Tn﹣1Pn﹣2Pn﹣1的面积,则S1+S2+S3+…+Sn﹣1=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:如果一个多边形的各个顶点均在另一个多边形的边上,则称这个多边形为另一多边形的内接多边形
问题探究:
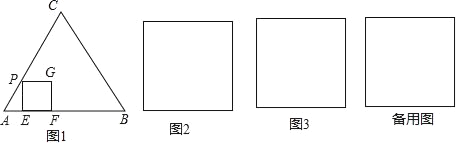
(1)如图1,正方形PEFG的顶点E、F在等边三角形ABC的边AB上,顶点P在AC边上.请在等边三角形ABC内部,以A为位似中心,作出正方形PEFG的位似正方形P'E'F'G',且使正方形P'E'F'G'的面积最大(不写作法)
(2)如图2,在边长为4正方形ABCD中,画出一个面积最大的内接正三角形,并求此最大内接正三角形的面积
拓展应用:
(3)如图3,在边长为4的正方形ABCD中,能不能截下一个面积最大的直角三角形,并使其三边比为3:4:5,若能,请求出此直角三角形的最大面积,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
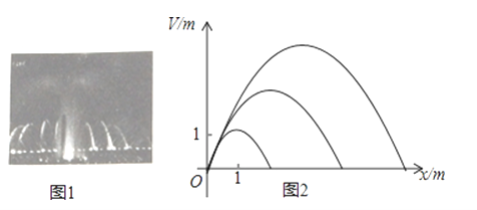
【题目】音乐喷泉(图1)可以使喷水造型随音乐的节奏起伏变化而变化.某种音乐喷泉形状如抛物线,设其出水口为原点,出水口离岸边18m,音乐变化时,抛物线的顶点在直线y=kx上变动,从而产生一组不同的抛物线(图2),这组抛物线的统一形式为y=ax2+bx.
(1)若已知k=1,且喷出的抛物线水线最大高度达3m,求此时a、b的值;
(2)若k=1,喷出的水恰好达到岸边,则此时喷出的抛物线水线最大高度是多少米?
(3)若k=3,a=﹣![]() ,则喷出的抛物线水线能否达到岸边?
,则喷出的抛物线水线能否达到岸边?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com