
【题目】求证:相似三角形面积的比等于相似比的平方.(请根据题意画出图形,写出已知,求证并证明)
【答案】证明见解析
【解析】
画出图形,写出已知,求证, 作AD⊥BC于D,A1D1⊥B1C1于D1然后根据相似三角形对应角可得∠B=∠B1, ∠BDA=∠B1D1A1,可得△ABD∽△A1B1D1, ![]() =k可得结论
=k可得结论
已知:如图,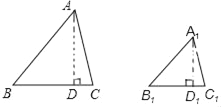
已知△ABC∽△A1B1C1,顶点A、B、C分别与A1、B1、C1对应,△ABC和△A1B1C1的相似比为k.
求证: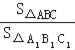 =k2;
=k2;
证明:作AD⊥BC于D,A1D1⊥B1C1于D1,
∵△ABC∽△A1B1C1,顶点A、B、C分别与A1、B1、C1对应,
∴∠B=∠B1,
∵AD、A1D1分别是△ABC,△A1B1C1的高线,
∴∠BDA=∠B1D1A1,
∴△ABD∽△A1B1D1,
∴![]() =k
=k
∴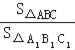 =
=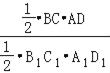 =k2.
=k2.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:①抛物线过原点; ②4a+b+c=0; ③a+b>0; ④该二次函数的最小值为b;⑤当0<x<4时,y>0.正确的是( )
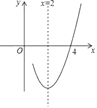
A. ①② B. ③④⑤ C. ①②④ D. ①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
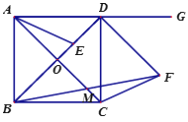
【题目】如图,已知正方形ABCD,对角线AC、BD交于点O,点E在对角线BD上,连接AE.点G是AD延长线上一点,DF平分∠GDC,且DF=BE,连接FB、FC,FB与AC交于点M.
(1)若点E是BD的三等分点(DE<BE),BF=![]() ,求△ABE的面积;
,求△ABE的面积;
(2)求证:DE=2CM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间 每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于340元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
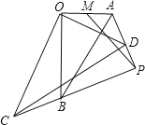
【题目】如图,Rt△AOB∽△DOC,∠AOB=∠COD=90°,M为OA的中点,OA=6,OB=8,将△COD绕O点旋转,连接AD,CB交于P点,连接MP,则MP的最小值____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学选拔一名青年志愿者:经笔试、面试,结果小明和小丽并列第一.评委会决定通过抓球来确定人选.规则如下:在不透明的布袋里装有除颜色之外均相同的2个红球和1个绿球,小明先取出一个球,记住颜色后放回,然后小丽再取出一个球.若两次取出的球都是红球,则小明胜出;若两次取出的球是一红一绿,则小丽胜出.你认为这个规则对双方公平吗?请用列表法或画树状图的方法进行分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
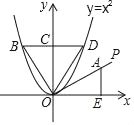
【题目】如图,射线OP与x轴正半轴的夹角为30°,点A是OP上一点,过点A作x轴的垂线与x轴交于点E.△AOE绕着点O逆时针旋转90°后能与△BOC重合,△BOC沿着y轴翻折能与△DOC重合,若点D恰好在抛物线y=x2(x>0)上,则点A的坐标是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com