
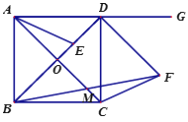
【题目】如图,已知正方形ABCD,对角线AC、BD交于点O,点E在对角线BD上,连接AE.点G是AD延长线上一点,DF平分∠GDC,且DF=BE,连接FB、FC,FB与AC交于点M.
(1)若点E是BD的三等分点(DE<BE),BF=![]() ,求△ABE的面积;
,求△ABE的面积;
(2)求证:DE=2CM.
【答案】(1)18;(2)证明见解析.
【解析】
(1)由点E是BD的三等分点,设BE=DF=2x,DE=x. 在Rt△BDF中,根据勾股定理得BD+DF=BF,即可求出![]() 的值,根据三角形的面积公式求解即可.
的值,根据三角形的面积公式求解即可.
(2)延长DF、BC交于点H.证明△EBA≌△FDC,根据全等三角形的性质得到AE=CF,∠AEB=∠CFD,再证明△AED≌△CFH,即可证明.
解:(1)由题意易得∠BDF=90°,
∵点E是BD的三等分点(DE<BE)
∴设BE=DF=2x,DE=x.
在Rt△BDF中,∠BDF=90°
∵BD+DF=BF
∴9x+4x=156解得x=![]()
∴BE=2x=![]() ,AO=
,AO=![]() BD=
BD=![]()
∴△ABE面积=![]() ·BE·AO=
·BE·AO=![]() =18.
=18.
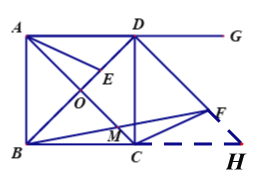
(2)同时延长DF、BC交于点H.
∵O是BD中点,OC∥DF
∴M是BF中点,C是BH中点.
∴CM是△BFH的中位线.
即FH=2CM.
在△EBA与△FDC中
EB=FD;∠ABE=∠FDC=45°,CD=AB
∴△EBA≌△FDC(SAS).
∴AE=CF,∠AEB=∠CFD
∴∠AED=∠CFH.
∵CM∥FH
∴∠H=∠ACB=∠ADB=45°.
在△AED与△CFH中
∠ADB=∠H,∠AED=∠CFH,AE=CF
∴△AED≌△CFH(AAS)
∴DE=FH=2CM.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】以直线x=1为对称轴的抛物线y=-x2+bx+c与x轴交于A、B两点,其中点A的坐标为(3,0).
(1)求点B的坐标;
(2)设点M(x1,y1)、N(x2,y2)在抛物线线上,且x1<x2<1,试比较y1、y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
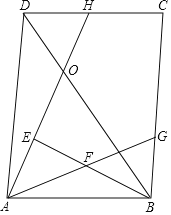
【题目】如图,在平行四边形ABCD中,点H为DC上一点,BD、AH交于点O,△ABO为等边三角形,点E在线段AO上,OD=OE,连接BE,点F为BE的中点,连接AF并延长交BC于点G,且∠GAD=60°.
(1)若CH=2,AB=4,求BC的长;
(2)求证:BD=AB+AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
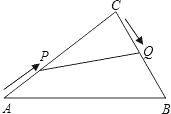
【题目】在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动.如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动,设运动的时间为t秒.
(1)用含t的代数式表示Rt△CPQ的面积S;
(2)当t=3秒时,P、Q两点之间的距离是多少?
(3)当t为多少秒时,以点C、P、Q为顶点的三角形与△ABC相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E为BC边上一点,连结AE.已知AB=8,CE=2,F是线段AE上一动点.若BF的延长线交正方形ABCD的一边于点G,且满足AE=BG,则![]() 的值为________.
的值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y (℃)与时间x(h)之间的函数关系,其中线段AB、BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)求这天的温度y与时间x(0≤x≤24)的函数关系式;
(2)求恒温系统设定的恒定温度;
(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:如果一个多边形的各个顶点均在另一个多边形的边上,则称这个多边形为另一多边形的内接多边形
问题探究:
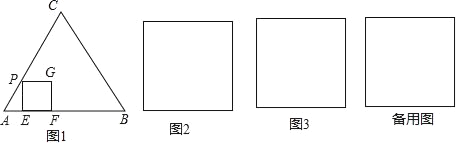
(1)如图1,正方形PEFG的顶点E、F在等边三角形ABC的边AB上,顶点P在AC边上.请在等边三角形ABC内部,以A为位似中心,作出正方形PEFG的位似正方形P'E'F'G',且使正方形P'E'F'G'的面积最大(不写作法)
(2)如图2,在边长为4正方形ABCD中,画出一个面积最大的内接正三角形,并求此最大内接正三角形的面积
拓展应用:
(3)如图3,在边长为4的正方形ABCD中,能不能截下一个面积最大的直角三角形,并使其三边比为3:4:5,若能,请求出此直角三角形的最大面积,若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com