
【题目】如图,在正方形ABCD中,E为BC边上一点,连结AE.已知AB=8,CE=2,F是线段AE上一动点.若BF的延长线交正方形ABCD的一边于点G,且满足AE=BG,则![]() 的值为________.
的值为________.

【答案】1或![]()
【解析】
根据题意进行分情况讨论,当点G在AD边上时,根据AE=BG,AB=AB, ∠BAG=∠ABE=90°,可证△ABG≌△BAE,可得AG=BE,根据AG∥BE,可得![]() ,当G’在CD上时,根据全等三角形的判定方法可证△ABE≌△BCG’可得∠BAE=∠CBG’,
,当G’在CD上时,根据全等三角形的判定方法可证△ABE≌△BCG’可得∠BAE=∠CBG’,
根据∠CBG’+∠ABF’=90°,可得∠BAE+∠ABF’=90°,继而可得: ∠AF’B=90°,可得BG’ ⊥AE,根据AB=8,BE=6,根据勾股定理可得:AE=10,根据等面积法可得:BF’=![]() ,F’G’=
,F’G’=![]() ,
,
可得![]() .
.
(1)当点G在AD边上时,
因为AE=BG,AB=AB, ∠BAG=∠ABE=90°,
所以△ABG≌△BAE,
所以AG=BE,
因为AG∥BE,
所以![]() ,
,
(2)当G’在CD上时,
同理可证△ABE≌△BCG’,
所以∠BAE=∠CBG’,
因为∠CBG’+∠ABF’=90°,
所以∠BAE+∠ABF’=90°,
所以 ∠AF’B=90°,
所以BG’ ⊥AE,
根据AB=8,BE=6,根据勾股定理可得:AE=10,
根据等面积法可得:BF’=![]() ,F’G’=
,F’G’=![]() ,
,
所以![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,二次函数y=﹣![]() +bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=﹣x+3与二次函数y=﹣
+bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=﹣x+3与二次函数y=﹣![]() +bx+c的图象分别交于B,C两点,点B在第一象限.
+bx+c的图象分别交于B,C两点,点B在第一象限.
(1)求二次函数y=﹣![]() +bx+c的表达式;
+bx+c的表达式;
(2)连接AB,求AB的长;
(3)连接AC,M是线段AC的中点,将点B绕点M旋转180°得到点N,连接AN,CN,判断四边形ABCN的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(m+3)x+m+1=0.
(1)求证:无论m取何值,原方程总有两个不相等的实数根;
(2)若x1,x2是原方程的两根,且|x1-x2|=2![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在四边形ABCD中,对角线AC、BD相交于点E,且AC⊥BD,作BF⊥CD,垂足为点F,BF与AC交于点C,∠BGE=∠ADE.
(1)如图1,求证:AD=CD;
(2)如图2,BH是△ABE的中线,若AE=2DE,DE=EG,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于△ADE面积的2倍.

查看答案和解析>>
科目:初中数学 来源: 题型:
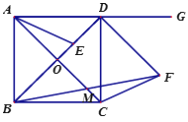
【题目】如图,已知正方形ABCD,对角线AC、BD交于点O,点E在对角线BD上,连接AE.点G是AD延长线上一点,DF平分∠GDC,且DF=BE,连接FB、FC,FB与AC交于点M.
(1)若点E是BD的三等分点(DE<BE),BF=![]() ,求△ABE的面积;
,求△ABE的面积;
(2)求证:DE=2CM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图①,在△ABC 中,∠BAC=90°,AB=AC,直线 m 经过点 A,BD⊥m 于点 D,CE⊥m 于点 E,求证:△ABD≌△CAE.
应用:如图②,在△ABC 中,AB=AC,D、A、E 三点都在直线 m 上,并且有∠BDA=∠AEC=∠BAC,求证:DE=BD+CE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间 每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于340元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x+m.
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com