
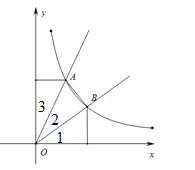
【题目】如图,以原点![]() 为端点的两条射线与反比例函数
为端点的两条射线与反比例函数![]() 交于
交于![]() 两点,且
两点,且![]() ,则
,则![]() 的面积是________.
的面积是________.
【答案】![]()
【解析】
由∠1=∠2=∠3,∠1+∠2+∠3=90°可得∠1=∠2=∠3=30°,再由特殊角的三角函数值、反比例函数比例系数|k| 可得S△AOD= S△EOB=3 ,S矩形ADOF=6,而S△AOD+ S△AOB+ S△EOB=S矩形ADOF+S梯形AFEB,A、B在双曲线![]() 上,所以S△AOD= S△EOB=3 ,S矩形ADOF=6
上,所以S△AOD= S△EOB=3 ,S矩形ADOF=6
所以S△AOB= S梯形AFEB而S梯形AFEB=![]() ·FE=
·FE=![]() ·(
·(![]() OA-
OA-![]() OA)
OA)
解得 S梯形AFEB=![]() =2
=2![]() 所以
所以 ![]() 的面积是2
的面积是2![]() .
.
解:

如图所示,作AD⊥y轴于D,BE⊥x轴于E,AF⊥x轴于F,
∵∠1=∠2=∠3,∠1+∠2+∠3=90°
∴∠1=∠2=∠3=30°
∴A(![]() OA,
OA,![]() OA),B(
OA),B(![]() OB,
OB,![]() OB)
OB)
∵A、B在![]() 上
上
∴![]() OA·
OA·![]() OA=6,
OA=6,![]() OB·
OB·![]() OB =6
OB =6
∴OA2= OB 2=8![]()
∵S△AOD+ S△AOB+ S△EOB=S矩形ADOF+S梯形AFEB,A、B在双曲线![]() 上
上
∴S△AOD= S△EOB=3 ,S矩形ADOF=6
∴S△AOB= S梯形AFEB
而S梯形AFEB=![]() ·FE=
·FE=![]() ·(
·(![]() OA-
OA-![]() OA)
OA)
∴ S梯形AFEB=![]() =2
=2![]()
![]() 的面积是2
的面积是2![]()
故答案为:2![]() .
.


科目:初中数学 来源: 题型:
【题目】游泳是一项深受青少年喜爱的体育活动,学校为了加强学生的安全意识,组织学生观看了纪实片“孩子,请不要私自下水”,并于观看后在本校的2000名学生中作了抽样调查.请根据下面两个不完整的统计图回答以下问题:
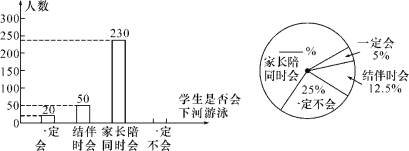
(1)这次抽样调查中,共调查了__ __名学生;
(2)补全两个统计图;
(3)根据抽样调查的结果,估算该校2000名学生中大约有多少人“一定会下河游泳”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E为BC边上一点,连结AE.已知AB=8,CE=2,F是线段AE上一动点.若BF的延长线交正方形ABCD的一边于点G,且满足AE=BG,则![]() 的值为________.
的值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是双曲线![]() 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
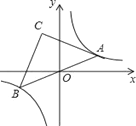
A. y=﹣![]() x B. y=﹣
x B. y=﹣![]() x C. y=﹣
x C. y=﹣![]() D. y=﹣
D. y=﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y (℃)与时间x(h)之间的函数关系,其中线段AB、BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)求这天的温度y与时间x(0≤x≤24)的函数关系式;
(2)求恒温系统设定的恒定温度;
(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四个命题:
①三角形的一条中线能将三角形分成面积相等的两部分;
②有两边和其中一边的对角对应相等的两个三角形全等;
③点P(1,2)关于原点的对称点坐标为(-1,-2);
④两圆的半径分别是3和4,圆心距为d,若两圆有公共点,则![]()
其中正确的是
A. ①② B.①③ C.②③ D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=3,BC=2,AC=AD,∠ACD=60°,则对角线BD长的最大值为( )
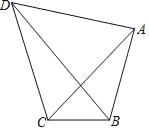
A. 5 B. 2![]() C. 2
C. 2![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
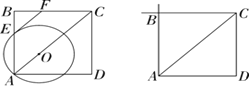
【题目】如图,点O在边长为6![]() 的正方形ABCD的对角线AC上,以O为圆心OA为半径的⊙O交AB于点E.
的正方形ABCD的对角线AC上,以O为圆心OA为半径的⊙O交AB于点E.
(1)⊙O过点E的切线与BC交于点F,当0<OA<6时,求∠BFE的度数;
(2)设⊙O与AB的延长线交于点M,⊙O过点M的切线交BC的延长线于点N,当6<OA<12时,利用备用图作出图形,求∠BNM的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com