
【题目】如图,点O在边长为6![]() 的正方形ABCD的对角线AC上,以O为圆心OA为半径的⊙O交AB于点E.
的正方形ABCD的对角线AC上,以O为圆心OA为半径的⊙O交AB于点E.
(1)⊙O过点E的切线与BC交于点F,当0<OA<6时,求∠BFE的度数;
(2)设⊙O与AB的延长线交于点M,⊙O过点M的切线交BC的延长线于点N,当6<OA<12时,利用备用图作出图形,求∠BNM的度数.
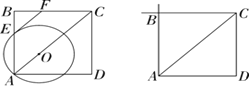
【答案】(1)∠BFE=45°;(2)∠BNM=45°.
【解析】
(1)连结OE,根据圆的半径都相等可得OA=OE,再根据等边对等角可得∠EAO=∠AEO,接下来再根据正方形以及切线性质即可得到∠BEF=45°,至此,再根据三角形内角和是180°即可得到∠BFE的度数了;
(2)根据题意画出图形,连结OM,根据等边对等角的性质和正方形的性质可得∠OAM=∠AMO=45°,至此,再根据切线的性质以及三角形内角和定理进行求解即可;
(1)连接OE,如解图,
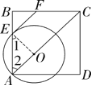
∵四边形ABCD为正方形,∴∠2=45°,
∵OE=OA,∴∠1=∠2=45°,
∵EF为⊙O的切线,∴OE⊥EF,
∴∠OEF=90°,∴∠BEF=45°,
∵∠B=90°,
∴∠BFE=45°;
(2)连接OM,如解图,
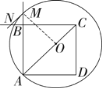
∵OM=OA,
∴∠OMA=∠OAM=45°,
∵MN为⊙O的切线,∴OM⊥MN,
∴∠OMN=90°,∴∠BMN=45°,
∵∠MBN=90°,∴∠BNM=45°.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x+m.
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
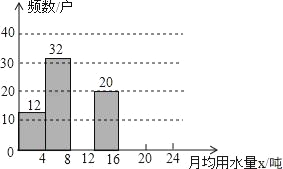
【题目】2014年,河北省委宣传部主办“河北节约之星”活动,表彰节水先进典型,省委宣传部号召全社会以节水先进典型为榜样,牢固树立节约用水理念,争做节俭美德的传承者,节约用水的践行者.小鹏想了解某小区住户月均用水情况,随机调查了该小区部分住户,并将调查数据绘制成如图所示的频数分布直方图(不完整)和如下的频数分布表.
月均用水量x(吨) | 频数(户) | 频率 |
0<x≤4 | 12 | a |
4<x≤8 | 32 | 0.32 |
8<x≤12 | b | c |
12<x≤16 | 20 | 0.2 |
16<x≤20 | 8 | 0.08 |
20<x≤24 | 4 | 0.04 |
(1)求a,b,c的值,并将如图所示的频数分布直方图补充完整;
(2)求月均用水量超过12吨的住户占所调查总住户的百分比;
(3)若该小区有1000住户,根据所调查的数据,该小区月均用水量没有超过8吨的住户有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
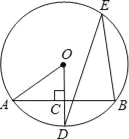
【题目】如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AB∥CD,AB=14,AD= 4![]() , CD=7.直线l经过A,D两点,且sin∠DAB=
, CD=7.直线l经过A,D两点,且sin∠DAB=![]() . 动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于AB,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
. 动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于AB,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
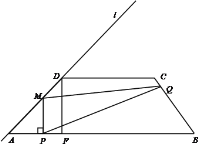
(1)求腰BC的长;
(2)当Q在BC上运动时,求S与t的函数关系式;
(3)在(2)的条件下,是否存在某一时刻t,使得△MPQ的面积S是梯形ABCD面积的![]() ?若存在,请求出t的值;若不存在,请说明理由;
?若存在,请求出t的值;若不存在,请说明理由;
(4)随着P,Q两点的运动,当点M在线段DC上运动时,设PM的延长线与直线l相交于点N,试探究:当t为何值时,△QMN为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
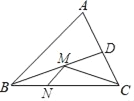
【题目】如图,在锐角三角形ABC中,BC=6![]() ,∠ABC=45°,BD平分∠ABC,M、N分别是BD、BC上的动点,则CM+MN的最小值是_____.
,∠ABC=45°,BD平分∠ABC,M、N分别是BD、BC上的动点,则CM+MN的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
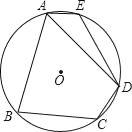
【题目】如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在![]() 上.
上.
(1)求∠E的度数;
(2)连接OD、OE,当∠DOE=90°时,AE恰好为⊙O的内接正n边形的一边,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是垂直于水平面的一棵树,小马(身高1.70米)从点
是垂直于水平面的一棵树,小马(身高1.70米)从点![]() 出发,先沿水平方向向左走10米到
出发,先沿水平方向向左走10米到![]() 点,再经过一段坡度
点,再经过一段坡度![]() ,坡长为5米的斜坡
,坡长为5米的斜坡![]() 到达
到达![]() 点,然后再沿水平方向向左行走5米到达
点,然后再沿水平方向向左行走5米到达![]() 点(
点(![]() 、
、![]() 、
、![]() 、
、![]() 在同一平面内),小马在线段
在同一平面内),小马在线段![]() 的黄金分割点
的黄金分割点![]() 处(
处(![]() )测得大树的顶端
)测得大树的顶端![]() 的仰角为37°,则大树
的仰角为37°,则大树![]() 的高度约为( )米.(参考数据:
的高度约为( )米.(参考数据:![]() )
)
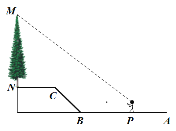
A. 7.8米 B. 8.0米 C. 8.1米 D. 8.3米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com