
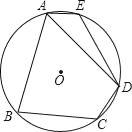
【题目】如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在![]() 上.
上.
(1)求∠E的度数;
(2)连接OD、OE,当∠DOE=90°时,AE恰好为⊙O的内接正n边形的一边,求n的值.
【答案】(1)∠AED=120°;(2)12.
【解析】试题分析:
(1)如图,连接BD,由已知条件证△ABD是等边三角形,得到∠ABD=60°,从而由圆内接四边形的性质可得∠AED=120°;
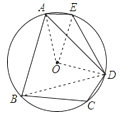
(2)如图,连接OA,由∠ABD=60°,可得∠AOD=120°,结合∠DOE=90°,可得∠AOE=30°,从而可得![]() .
.
试题解析:
(1)如图,连接BD,
∵四边形ABCD是⊙O的内接四边形,
∴∠BAD+∠C=180°,
∵∠C=120°,
∴∠BAD=60°,
∵AB=AD,
∴△ABD是等边三角形,
∴∠ABD=60°,
∵四边形ABDE是⊙O的内接四边形,
∴∠AED+∠ABD=180°,
∴∠AED=120°;
(2)连接OA,
∵∠ABD=60°,
∴∠AOD=2∠ABD=120°,
∵∠DOE=90°,
∴∠AOE=∠AOD﹣∠DOE=30°,
∴![]() .
.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
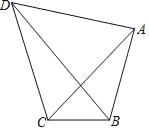
【题目】如图,四边形ABCD中,AB=3,BC=2,AC=AD,∠ACD=60°,则对角线BD长的最大值为( )
A. 5 B. 2![]() C. 2
C. 2![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
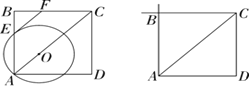
【题目】如图,点O在边长为6![]() 的正方形ABCD的对角线AC上,以O为圆心OA为半径的⊙O交AB于点E.
的正方形ABCD的对角线AC上,以O为圆心OA为半径的⊙O交AB于点E.
(1)⊙O过点E的切线与BC交于点F,当0<OA<6时,求∠BFE的度数;
(2)设⊙O与AB的延长线交于点M,⊙O过点M的切线交BC的延长线于点N,当6<OA<12时,利用备用图作出图形,求∠BNM的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,点Q坐标为(x,y),若过点Q的直线l与x轴夹角为45°时,则称直线l为点Q的“湘依直线”.
(1)已知点A的坐标为(6,0),求点A的“湘依直线”表达式;
(2)已知点D的坐标为(0,﹣4),过点D的“湘依直线”图象经过第二、三、四象限,且与x轴交于C点,动点P在反比例函数y=![]() (x>0)上,求△PCD面积的最小值及此时点P的坐标;
(x>0)上,求△PCD面积的最小值及此时点P的坐标;
(3)已知点M的坐标为(0,2),经过点M且在第一、二、三象限的“湘依直线”与抛物线y=x2+(m﹣2)x+m+2相交与A(x1,y1),B(x2,y2)两点,若0≤x1≤2,0≤x2≤2,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
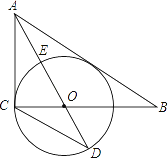
(1)求证:AB是⊙O的切线.
(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD=![]() ,求
,求![]() 的值.
的值.
(3)在(2)的条件下,设⊙O的半径为3,求AB的长.
【答案】(1)证明见解析(2)![]() (3)
(3)![]()
【解析】试题分析:(1)过O作OF⊥AB于F,由角平分线上的点到角两边的距离相等即可得证;(2)连接CE,证明△ACE∽△ADC可得![]() = tanD=
= tanD=![]() ;(3)先由勾股定理求得AE的长,再证明△B0F∽△BAC,得
;(3)先由勾股定理求得AE的长,再证明△B0F∽△BAC,得![]() ,设BO="y" ,BF=z,列二元一次方程组即可解决问题.
,设BO="y" ,BF=z,列二元一次方程组即可解决问题.
试题解析:(1)证明:作OF⊥AB于F
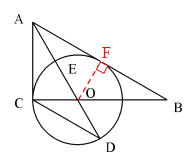
∵AO是∠BAC的角平分线,∠ACB=90
∴OC=OF
∴AB是⊙O的切线
(2)连接CE
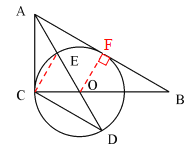
∵AO是∠BAC的角平分线,
∴∠CAE=∠CAD
∵∠ACE所对的弧与∠CDE所对的弧是同弧
∴∠ACE=∠CDE
∴△ACE∽△ADC
∴![]() = tanD=
= tanD=![]()
(3)先在△ACO中,设AE=x,
由勾股定理得
(x+3)="(2x)" +3 ,解得x="2,"
∵∠BFO=90°=∠ACO
易证Rt△B0F∽Rt△BAC
得![]() ,
,
设BO=y BF=z
![]()
即4z=9+3y,4y=12+3z
解得z=![]() y=
y=![]()
∴AB=![]() +4=
+4=![]()
考点:圆的综合题.
【题型】解答题
【结束】
22
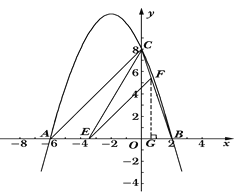
【题目】已知:二次函数![]() 的图象与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段O、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且A点坐标为(-6,0).
的图象与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段O、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且A点坐标为(-6,0).
(1)求此二次函数的表达式;
(2)若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=![]() .对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
(1)证明:当旋转角为90°时,四边形ABEF是平行四边形;
(2)试说明在旋转过程中,线段AF与EC总保持相等;
(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时AC绕点O顺时针旋转的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
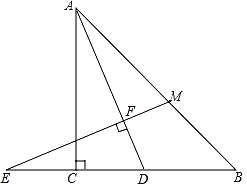
【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AC=BC,D是线段BC上一动点(不与点B、C重合),连接AD,延长BC至点E,使得CE=CD,过点E作EF⊥AD于点F,再延长EF交AB于点M.
(1)若D为BC的中点,AB=4,求AD的长;
(2)求证:BM=![]() CD.
CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
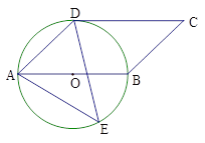
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上任意一点,且CD切⊙O于点D.
(1)试求∠AED的度数.
(2)若⊙O的半径为![]() cm,试求△ADE面积的最大值.
cm,试求△ADE面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,市防汛指挥部决定对某水库的水坝进行加高加固,设计师提供的方案是:水坝加高1米(EF=1米),背水坡AF的坡度i=1∶1,已知AB=3米,∠ABE=120°,求水坝原来的高度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com