
����Ŀ�����壺��ƽ��ֱ������ϵ�У���Q����Ϊ��x��y����������Q��ֱ��l��x��н�Ϊ45��ʱ�����ֱ��lΪ��Q�ġ�����ֱ�ߡ���
��1����֪��A������Ϊ��6��0�������A�ġ�����ֱ�ߡ�����ʽ��
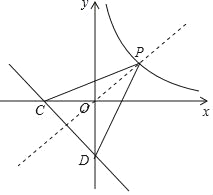
��2����֪��D������Ϊ��0����4��������D�ġ�����ֱ�ߡ�ͼ���ڶ������������ޣ�����x�ύ��C�㣬����P�ڷ���������y=![]() ��x��0���ϣ����PCD�������Сֵ����ʱ��P�����ꣻ
��x��0���ϣ����PCD�������Сֵ����ʱ��P�����ꣻ
��3����֪��M������Ϊ��0��2����������M���ڵ�һ�����������ġ�����ֱ�ߡ���������y=x2+��m��2��x+m+2�ཻ��A��x1��y1����B��x2��y2�����㣬��0��x1��2��0��x2��2����m��ȡֵ��Χ��
���𰸡���1��y=x��6��y=��x+6����2����PCD�������Сֵ��24����ʱ��P�������ǣ�4��4������3��m��ȡֵ��Χ��1��m��3��
��������
��1���ɡ�����ֱ�ߡ��Ķ���֪��ֱ��l��ֱ��y=x��y=��xƽ�У����A�ġ�����ֱ�ߡ�����ʽΪ��y=x+b��y=��x+b����A��6�� 0�����룬��0=6+b����0=��6+b���ɴ����bֵ���������A�ġ�����ֱ�ߡ�����ʽ����2������ù���D�ġ�����ֱ�ߡ�Ϊy=��x��4�������C�������Ϊ����4��0�������ɵá�OCD�ǵ���ֱ�������Σ�����CD=4![]() ����Ϊ�߶�CD�ij���Ϊ��ֵ����֪������P��ֱ����ֱ��CD��ֱʱ����PCD�������С���ɴ˼��ɽ�𣻣�3����ù���M�ġ�����ֱ�ߡ�Ϊy=x+2���������ߵĽ���ʽ����M�ġ�����ֱ�ߡ������������ɵ�x2+��m��3��x+m=0�����ݸ���ϵ���Ĺ�ϵ��x1+x2=3��m��x1x2=m����0��x1��2��0��x2��2����֪0��x1+x2��4��0��x1x2��4�ң�m��3��2��4m��0���ɴ˼������m��ȡֵ��Χ.
����Ϊ�߶�CD�ij���Ϊ��ֵ����֪������P��ֱ����ֱ��CD��ֱʱ����PCD�������С���ɴ˼��ɽ�𣻣�3����ù���M�ġ�����ֱ�ߡ�Ϊy=x+2���������ߵĽ���ʽ����M�ġ�����ֱ�ߡ������������ɵ�x2+��m��3��x+m=0�����ݸ���ϵ���Ĺ�ϵ��x1+x2=3��m��x1x2=m����0��x1��2��0��x2��2����֪0��x1+x2��4��0��x1x2��4�ң�m��3��2��4m��0���ɴ˼������m��ȡֵ��Χ.
�ɡ�����ֱ�ߡ��Ķ���֪��ֱ��l��ֱ��y=x��y=��xƽ�У�
��1�����A�ġ�����ֱ�ߡ�����ʽΪ��y=x+b��y=��x+b��
��A��6�� 0�����룬��0=6+b����0=��6+b
���b=��6��b=6��
�ʵ�A�ġ�����ֱ�ߡ�����ʽΪ��y=x��6��y=��x+6��
��2���ߵ�D������Ϊ��0����4��������D�ġ�����ֱ�ߡ�ͼ���ڶ������������ޣ�
�����D�ġ�����ֱ�ߡ�Ϊy=��x��4��
��C����4��0��������OCD�ǵ���ֱ�������Σ�
��CD=4![]() ��
��
���߶�CD�ij���Ϊ��ֵ��
�൱����P��ֱ����ֱ��CD��ֱʱ����PCD�������С��
�֡ߵ�P�ڷ���������y=![]() ��x��0��ͼ���ϣ�
��x��0��ͼ���ϣ�
���P���߶�CD�Ĵ�ֱƽ������˫���ߵĽ��㣬��ͼ��
��ֱ��CD��ֱ��y=��xƽ�У�
���P��ֱ��y=x�ϣ�
����P��a��a����
��a=![]() ��
��
���a=4����ȥ��ֵ����
��ʱP��4��4����
S��PCD=![]() ��4
��4![]() ����4
����4![]() +2
+2![]() ��=24��
��=24��
������������PCD�������Сֵ��24����ʱ��P�������ǣ�4��4����
��3���ߵ�M������Ϊ��0��2��������M�ġ�����ֱ�ߡ�������һ�����������ޣ�
�����M�ġ�����ֱ�ߡ�Ϊy=x+2��
��������֪��![]()
��������x2+��m��3��x+m=0
��x1+x2=3��m��x1x2=m��
��0��x1��2��0��x2��2��
��0��x1+x2��4��0��x1x2��4�ң�m��3��2��4m��0��
��0��3��m��4��0��m��4�ң�m��3��2��4m��0��
��ã�1��m��3��
��m��ȡֵ��Χ��1��m��3��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��O������ԭ�㣬����������y=![]() ��ͼ��A(
��ͼ��A(![]() ,1)��
,1)��
��1����˷����������Ľ���ʽ��
��2�����߶�OA��O��ʱ����ת30��õ��߶�OB���жϵ�B�Ƿ��ڴ˷�����������ͼ���ϲ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
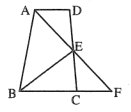
����Ŀ����֪����Rt��ABC�У���ACB��90����AB��AC����D��ֱ��AB�ϣ�����CD����CD���Ҳ���CE��CD��CD��CE��
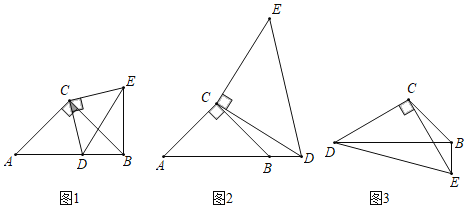
��1����ͼ1���ٵ�D��AB���ϣ�ֱ��д���߶�BE���߶�AD�Ĺ�ϵ��
��2����ͼ2����D��B�Ҳ࣬BD��1��BE��5����CE�ij���
��3����չ����
��ͼ3����DCE����DBE��90��CD��CE��BC��![]() ��BE��1����ֱ��д���߶�EC�ij���
��BE��1����ֱ��д���߶�EC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ѽ���ͼ��ƴ��һ���µ�ͼ�Σ���ͨ��ͼ������ļ��㣬�������Եõ�һЩ���õ�ʽ�ӣ���������һЩ������ͼ�ε������
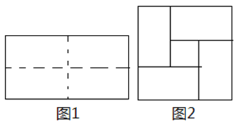
��1��ѡ���⣺ͼ1��һ����2a����2b��a��b���ij����Σ��ü�����ͼ�����ߣ��Գ��ᣩ�����������ֳ��Ŀ���״�ʹ�С��һ����С�����Σ�Ȼ��ͼ2����ƴ��һ�����м�յģ������Σ����м�յIJ�������ǣ��� ��
A��2ab B����a+b��2 C����a��b��2 D��a2��b2
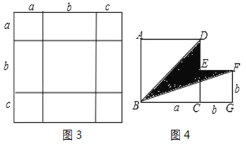
��2����ͼ3���ǽ�����������ȵ�С��������С������ƴ��һ���߳�Ϊa+b+c�������Σ����ò�ͬ�ķ����������ͼ�ε�������ݴˣ����ܷ���ʲô���ۣ���ֱ��д��������
��3����ͼ4���ǽ������߳��ֱ�Ϊa��b��������ƴ��һ��B��C��G������ͬһֱ���ϣ�����BD��BF�������������εı߳�����a+b=10��ab=20������Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �ǵ�һ�����ڵĵ㣬ֱ��
�ǵ�һ�����ڵĵ㣬ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() �Ḻ�����ڵ�
�Ḻ�����ڵ�![]() ������
������![]() ��
��![]() ��
��

��1����![]() �������
�������
��2�����![]() �������
�������![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����л����崫ͳ�Ļ���ij�оٰ�����Сѧ������ѧ�����������������ĿΪ��A����ʫ��B���δʣ�C�����D�����־���������ʽ����������������˫��������
��1��С���μ������������������������ȡһ��������Ŀ��ǡ�ó������������ĸ����Ƕ��٣�
��2��С����С�����һ��С��μ���˫���������������������ǣ�ͬһС���������Ա�ı�����Ŀ������ͬ����ÿ��ֻ�������ȡһ�Σ���ǡ��С����������ʫ����С��������δ����ĸ����Ƕ��٣�С����С�춼û�г鵽�����־����ĸ����Ƕ��٣����û���״ͼ���б��ķ�������˵����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ͬѧ��������Ϸ�����ǰ������ֱ����1��2��3�Ĵ�С����״��ȫ��ͬ��С�����һ�������Ŀڴ��У�
��1����Ӵ����������һ�����1�ĸ��ʣ�
��2���Ӵ����������һ���Żأ�ҡ�Ⱥ����������һ����������������ı��֮��Ϊż��ʱ�����ʤ����������������ı��֮��Ϊ����ʱ������ʤ���Է��������Ϸ�Ƿ�ƽ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���![]() �У�
��![]() ��
��![]() Ϊ
Ϊ![]() ���е㣬����
���е㣬����![]() ���ӳ���
���ӳ���![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ������
������![]() ƽ��
ƽ��![]() �����н��ۣ���
�����н��ۣ���![]() ����
����![]() ��ֱƽ��
��ֱƽ��![]() ����
����![]() ����
����![]() ��������ȷ����_____________��
��������ȷ����_____________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com