
【题目】已知:在Rt△ABC中,∠ACB=90°,AB=AC,点D在直线AB上,连接CD,在CD的右侧作CE⊥CD,CD=CE,
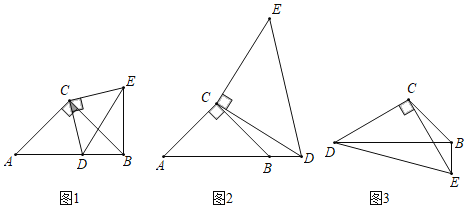
(1)如图1,①点D在AB边上,直接写出线段BE和线段AD的关系;
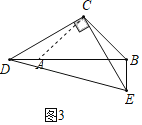
(2)如图2,点D在B右侧,BD=1,BE=5,求CE的长.
(3)拓展延伸
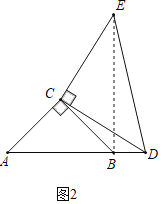
如图3,∠DCE=∠DBE=90,CD=CE,BC=![]() ,BE=1,请直接写出线段EC的长.
,BE=1,请直接写出线段EC的长.
【答案】(1)AD⊥BE;(2)CE=![]() ;(3)CE=
;(3)CE=![]() .
.
【解析】
(1)根据全等三角形的性质得到AD=BE,∠A=∠CBE,求得∠ABE=90°,于是得到结论;
(2)如图2,连接BE,根据全等三角形的性质得到∠A=∠CBE,推出∠DBE=90°,根据勾股定理得到DE=![]() =
=![]() =
=![]() ,即可得到结论;
,即可得到结论;
(3)如图3,过C作CA⊥BC交DB于A,根据已知条件得到D,E,B,C四点共圆,求得∠CDA=∠CEB,根据全等三角形的性质得到AD=BE=1,AC=BC,得到△ACB是等腰直角三角形,于是得到结论.
解:(1)∵∠ACB=∠DCE=90°,
∴∠ACD=∠BCE,
∵AC=BC,CD=CE,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠A=∠CBE,
∵∠A+∠ABC=90°,
∴∠ABE=90°,
∴AD⊥BE;
(2)如图2,连接BE,∵∠ACB=∠DCE=90°,
∴∠ACD=∠BCE,
∵AC=BC,CD=CE,
∴△ACD≌△BCE(SAS),
∴∠A=∠CBE,
∵∠A+∠ABC=90°,
∴∠ABE=90°,
∴∠DBE=90°,
∵BD=1,BE=5,
∴DE=![]() =
=![]() =
=![]() ,
,
∵CD=CE,∠DCE=90°,
∴CE=![]() DE=
DE=![]() ;
;
(3)如图3,过C作CA⊥BC交DB于A,
∵∠DCE=90°,
∴∠DCA=∠ECB,
∵∠DCE=∠DBE=90°,
∴D,E,B,C四点共圆,
∴∠CDA=∠CEB,
∵CD=CE,
∴△CDA≌△CEB(ASA),
∴AD=BE=1,AC=BC,
∴△ACB是等腰直角三角形,
∴AB=![]() BC=2,
BC=2,
∴BD=3,
∴DE=![]() =
=![]() =
=![]() ,
,
∴CE=![]() DE=
DE=![]() .
.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】(1)已知二次函数![]() 的图象经过点(﹣2,8)和(﹣1,5),求这个二次函数的表达式;
的图象经过点(﹣2,8)和(﹣1,5),求这个二次函数的表达式;
(2)已知抛物线的顶点为(﹣1,﹣3),与y轴的交点为(0,﹣5),求这个抛物线相应的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
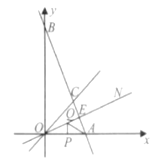
【题目】如下图,在平面直角坐标系中,直线AB与x轴交于点A,与y轴交于点B,与直线OC:y=x交于点C.
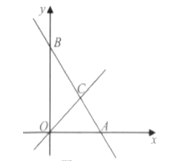
(1)若直线AB解析式为![]() .
.
①求点C的坐标;
②根据图象,求关于x的不等式0<-![]() x+10<x的解集;
x+10<x的解集;
(2)如下图,作∠AOC的平分线ON,若AB⊥ON,垂足为E,ΔOAC的面积为9,且OA=6,P、Q分别为线段OA、OE上的动点,连接AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值:若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高服务质量,某宾馆决定对甲、乙两种套房进行星级提升,已知甲种套房提升费用比乙种套房提升费用少3万元,如果提升相同数量的套房,甲种套房费用为625万元,乙种套房费用为700万元.
(1)甲、乙两种套房每套提升费用各多少万元?
(2)如果需要甲、乙两种套房共80套,市政府筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于甲、乙种套房星级提升,市政府对两种套房的提升有几种方案?哪一种方案的提升费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,AD是∠BAC的角平分线,若AB=AC+CD.那么∠ACB 与∠ABC有怎样的数量关系? 小明通过观察分析,形成了如下解题思路:

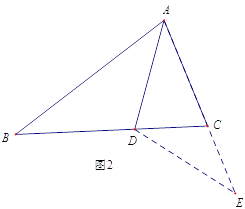
如图2,延长AC到E,使CE=CD,连接DE,由AB=AC+CD,可得AE=AB,又因为AD是∠BAC的平分线,可得△ABD≌△AED,进一步分析就可以得到∠ACB 与∠ABC的数量关系.
(1) 判定△ABD 与△AED 全等的依据是______________(SSS,SAS,ASA,AAS 从其中选择一个);
(2)∠ACB 与∠ABC的数量关系为:___________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,点Q坐标为(x,y),若过点Q的直线l与x轴夹角为45°时,则称直线l为点Q的“湘依直线”.
(1)已知点A的坐标为(6,0),求点A的“湘依直线”表达式;
(2)已知点D的坐标为(0,﹣4),过点D的“湘依直线”图象经过第二、三、四象限,且与x轴交于C点,动点P在反比例函数y=![]() (x>0)上,求△PCD面积的最小值及此时点P的坐标;
(x>0)上,求△PCD面积的最小值及此时点P的坐标;
(3)已知点M的坐标为(0,2),经过点M且在第一、二、三象限的“湘依直线”与抛物线y=x2+(m﹣2)x+m+2相交与A(x1,y1),B(x2,y2)两点,若0≤x1≤2,0≤x2≤2,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
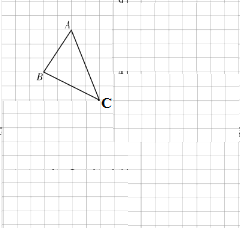
【题目】已知,在边长为1的小正方形组成的网格中,点![]() .
.
(1)在网格中正确画出平面直角坐标系;
(2)在平面直角坐标系中作出![]() 关于
关于![]() 轴对称的图形
轴对称的图形![]() ,并将点
,并将点![]() 先向右平移4个单位长度再向下平移1个单位长度得到点
先向右平移4个单位长度再向下平移1个单位长度得到点![]() ,写出点
,写出点![]() 的坐标;
的坐标;
(3)顺次连接点![]() 得到
得到![]() ,
,![]() 是等腰直角三角形吗?请说明理由.
是等腰直角三角形吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com