
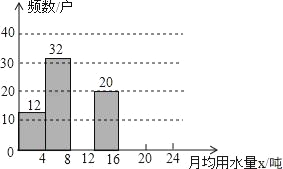
【题目】2014年,河北省委宣传部主办“河北节约之星”活动,表彰节水先进典型,省委宣传部号召全社会以节水先进典型为榜样,牢固树立节约用水理念,争做节俭美德的传承者,节约用水的践行者.小鹏想了解某小区住户月均用水情况,随机调查了该小区部分住户,并将调查数据绘制成如图所示的频数分布直方图(不完整)和如下的频数分布表.
月均用水量x(吨) | 频数(户) | 频率 |
0<x≤4 | 12 | a |
4<x≤8 | 32 | 0.32 |
8<x≤12 | b | c |
12<x≤16 | 20 | 0.2 |
16<x≤20 | 8 | 0.08 |
20<x≤24 | 4 | 0.04 |
(1)求a,b,c的值,并将如图所示的频数分布直方图补充完整;
(2)求月均用水量超过12吨的住户占所调查总住户的百分比;
(3)若该小区有1000住户,根据所调查的数据,该小区月均用水量没有超过8吨的住户有多少?
【答案】(1)a=0.12;b=24;c=0.24;(2)32%;(3)440户.
【解析】
(1)根据4<x≤8的频数和频率求出总数,再用0<x≤4的频数乘以总数求出a,用总数减去其它月均用水量求出8<x≤12的频数,即b的值,用B的值除以总数即可求出c,从而补全统计图;
(2)把月均用水量超过12吨的住户的频率加起来即可得出答案;
(3)用该小区的住户乘以月均用水量没有超过8吨的百分比即可得出答案.
(1)根据题意得:![]() =100(吨),
=100(吨),
则a=![]() =0.12;
=0.12;
b=100﹣12﹣32﹣20﹣8﹣4=24;
c=![]() =0.24;
=0.24;
补图如下:
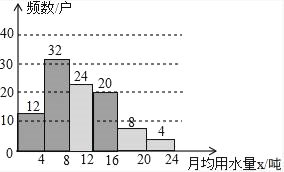
(2)月均用水量超过12吨的住户占所调查总住户的百分比是:0.2+0.08+0.04=0.32=32%;
(3)根据题意得:
1000×(0.12+0.32)=440(户),
答:该小区月均用水量没有超过8吨的住户有440户.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,点A是双曲线![]() 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
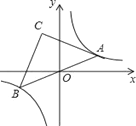
A. y=﹣![]() x B. y=﹣
x B. y=﹣![]() x C. y=﹣
x C. y=﹣![]() D. y=﹣
D. y=﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=3,BC=2,AC=AD,∠ACD=60°,则对角线BD长的最大值为( )
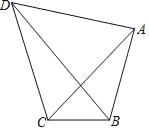
A. 5 B. 2![]() C. 2
C. 2![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
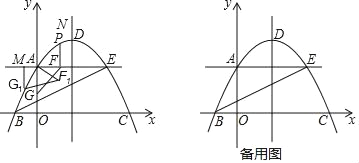
【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)求C、D两点坐标及△BCD的面积;
(3)若点P在x轴上方的抛物线上,满足S△PCD=![]() S△BCD,求点P的坐标.
S△BCD,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点为D的抛物线y=﹣![]() x2+
x2+![]() x+4与y轴交于点A,与x轴交于两点B、C(点B在点C的左边),点A与点E关于抛物线的对称轴对称,点B、E在直线y=kx+b(k,b为常数)上.
x+4与y轴交于点A,与x轴交于两点B、C(点B在点C的左边),点A与点E关于抛物线的对称轴对称,点B、E在直线y=kx+b(k,b为常数)上.
(1)求k,b的值;
(2)点P为直线AE上方抛物线上的任意一点,过点P作AE的垂线交AE于点F,点G为y轴上任意一点,当△PBE的面积最大时,求PF+FG+![]() OG的最小值;
OG的最小值;
(3)在(2)中,当PF+FG+![]() OG取得最小值时,将△AFG绕点A按顺时方向旋转30°后得到△AF1G1,过点G1作AE的垂线与AE交于点M.点D向上平移
OG取得最小值时,将△AFG绕点A按顺时方向旋转30°后得到△AF1G1,过点G1作AE的垂线与AE交于点M.点D向上平移![]() 个单位长度后能与点N重合,点Q为直线DN上任意一点,在平面直角坐标系中是否存在一点S,使以S、Q、M、N为顶点且MN为边的四边形为菱形?若存在,直接写出点S的坐标;若不存在,请说明理由.
个单位长度后能与点N重合,点Q为直线DN上任意一点,在平面直角坐标系中是否存在一点S,使以S、Q、M、N为顶点且MN为边的四边形为菱形?若存在,直接写出点S的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
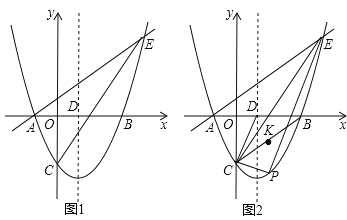
(1)求直线AE的解析式;
(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是CP上的一点,点N是CD上的一点,求KM+MN+NK的最小值;
(3)点G是线段CE的中点,将抛物线y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
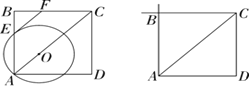
【题目】如图,点O在边长为6![]() 的正方形ABCD的对角线AC上,以O为圆心OA为半径的⊙O交AB于点E.
的正方形ABCD的对角线AC上,以O为圆心OA为半径的⊙O交AB于点E.
(1)⊙O过点E的切线与BC交于点F,当0<OA<6时,求∠BFE的度数;
(2)设⊙O与AB的延长线交于点M,⊙O过点M的切线交BC的延长线于点N,当6<OA<12时,利用备用图作出图形,求∠BNM的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,点Q坐标为(x,y),若过点Q的直线l与x轴夹角为45°时,则称直线l为点Q的“湘依直线”.
(1)已知点A的坐标为(6,0),求点A的“湘依直线”表达式;
(2)已知点D的坐标为(0,﹣4),过点D的“湘依直线”图象经过第二、三、四象限,且与x轴交于C点,动点P在反比例函数y=![]() (x>0)上,求△PCD面积的最小值及此时点P的坐标;
(x>0)上,求△PCD面积的最小值及此时点P的坐标;
(3)已知点M的坐标为(0,2),经过点M且在第一、二、三象限的“湘依直线”与抛物线y=x2+(m﹣2)x+m+2相交与A(x1,y1),B(x2,y2)两点,若0≤x1≤2,0≤x2≤2,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
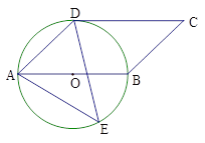
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上任意一点,且CD切⊙O于点D.
(1)试求∠AED的度数.
(2)若⊙O的半径为![]() cm,试求△ADE面积的最大值.
cm,试求△ADE面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com