
【题目】如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆C,点B是该半圆周上一动点,连接OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴、直线OB于点E、F,点E为垂足,连接CF. 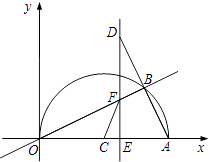
(1)当∠AOB=30°时,求弧AB的长度;
(2)当DE=8时,求线段EF的长;
(3)在点B运动过程中,是否存在以点E、C、F为顶点的三角形与△AOB相似?若存在,请求出此时点E的坐标;若不存在,请说明理由.
【答案】
(1)解:连接BC,
∵A(10,0),∴OA=10,CA=5,
∵∠AOB=30°,
∴∠ACB=2∠AOB=60°,
∴弧AB的长= ![]()
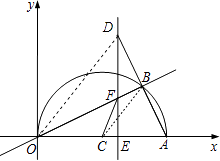
(2)解:①若D在第一象限,
连接OD,
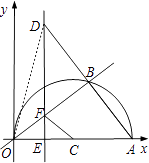
∵OA是⊙C直径,
∴∠OBA=90°,
又∵AB=BD,
∴OB是AD的垂直平分线,
∴OD=OA=10,
在Rt△ODE中,
OE= ![]() =
= ![]() ,
,
∴AE=AO﹣OE=10﹣6=4,
由∠AOB=∠ADE=90°﹣∠OAB,∠OEF=∠DEA,
得△OEF∽△DEA,
∴ ![]() ,即
,即 ![]() ,
,
∴EF=3;
②若D在第二象限,
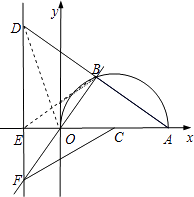
连接OD,
∵OA是⊙C直径,
∴∠OBA=90°,
又∵AB=BD,
∴OB是AD的垂直平分线,
∴OD=OA=10,
在Rt△ODE中,
OE= ![]() =
= ![]() ,
,
∴AE=AO+OE=10+6=16,
由∠AOB=∠ADE=90°﹣∠OAB,∠OEF=∠DEA,
得△OEF∽△DEA,
∴ ![]() ,即
,即 ![]() =
= ![]() ,
,
∴EF=12;
∴EF=3或12;
(3)解:设OE=x,
①当交点E在O,C之间时,由以点E、C、F为顶点的三角
形与△AOB相似,有∠ECF=∠BOA或∠ECF=∠OAB,
当∠ECF=∠BOA时,此时△OCF为等腰三角形,点E为OC
中点,即OE= ![]() ,
,
∴E1( ![]() ,0);
,0);
当∠ECF=∠OAB时,有CE=5﹣x,AE=10﹣x,
∴CF∥AB,有CF= ![]() ,
,
∵△ECF∽△EAD,
∴ ![]() ,即
,即 ![]() ,解得:
,解得: ![]() ,
,
∴E2( ![]() ,0);
,0);
②当交点E在点C的右侧时,
∵∠ECF>∠BOA,
∴要使△ECF与△BAO相似,只能使∠ECF=∠BAO,
连接BE,
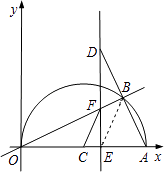
∵BE为Rt△ADE斜边上的中线,
∴BE=AB=BD,
∴∠BEA=∠BAO,
∴∠BEA=∠ECF,
∴CF∥BE,
∴ ![]() ,
,
∵∠ECF=∠BAO,∠FEC=∠DEA=90°,
∴△CEF∽△AED,
∴ ![]() ,
,
而AD=2BE,
∴ ![]() ,
,
即 ![]() ,解得
,解得 ![]() <0(舍去),
<0(舍去),
∴E3( ![]() ,0);
,0);
③当交点E在点O的左侧时,
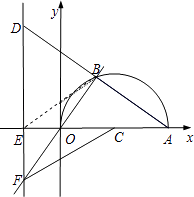
∵∠BOA=∠EOF>∠ECF.
∴要使△ECF与△BAO相似,只能使∠ECF=∠BAO
连接BE,得BE= ![]() =AB,∠BEA=∠BAO
=AB,∠BEA=∠BAO
∴∠ECF=∠BEA,
∴CF∥BE,
∴ ![]() ,
,
又∵∠ECF=∠BAO,∠FEC=∠DEA=90°,
∴△CEF∽△AED,
∴ ![]() ,
,
而AD=2BE,
∴ ![]() ,
,
∴ ![]() ,
,
解得x1= ![]() ,x2=
,x2= ![]() (舍去),
(舍去),
∵点E在x轴负半轴上,
∴E4( ![]() ,0),
,0),
综上所述:存在以点E、C、F为顶点的三角形与△AOB相似,
此时点E坐标为:E1( ![]() ,0)、E2(
,0)、E2( ![]() ,0)、E3(
,0)、E3( ![]() ,0)、E4(
,0)、E4( ![]() ,0).
,0).
【解析】(1)连接BC,由已知得∠ACB=2∠AOB=60°,AC= ![]() AO=5,根据弧长公式求解;(2)连接OD,由垂直平分线的性质得OD=OA=10,又DE=8,在Rt△ODE中,由勾股定理求OE,依题意证明△OEF∽△DEA,利用相似比求EF;(3)存在.当以点E、C、F为顶点的三角形与△AOB相似时,分为①当交点E在O,C之间时,由以点E、C、F为顶点的三角形与△AOB相似,有∠ECF=∠BOA或∠ECF=∠OAB,②当交点E在点C的右侧时,要使△ECF与△BAO相似,只能使∠ECF=∠BAO,③当交点E在点O的左侧时,要使△ECF与△BAO相似,只能使∠ECF=∠BAO,三种情况,分别求E点坐标.
AO=5,根据弧长公式求解;(2)连接OD,由垂直平分线的性质得OD=OA=10,又DE=8,在Rt△ODE中,由勾股定理求OE,依题意证明△OEF∽△DEA,利用相似比求EF;(3)存在.当以点E、C、F为顶点的三角形与△AOB相似时,分为①当交点E在O,C之间时,由以点E、C、F为顶点的三角形与△AOB相似,有∠ECF=∠BOA或∠ECF=∠OAB,②当交点E在点C的右侧时,要使△ECF与△BAO相似,只能使∠ECF=∠BAO,③当交点E在点O的左侧时,要使△ECF与△BAO相似,只能使∠ECF=∠BAO,三种情况,分别求E点坐标.


科目:初中数学 来源: 题型:
【题目】某汽车行驶时油箱中余油量Q(L)与行驶时间t(h)的关系如表:
行驶时间t/h | 余油量Q/L |
1 | 42 |
2 | 34 |
3 | 26 |
4 | 18 |
5 | 10 |
(1)汽车行驶之前油箱中有汽油多少升?
(2)用行驶时间t的代数式表示余油量Q(直接写出答案);
(3)当t=![]() 时,求余油量Q的值.
时,求余油量Q的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生活经验表明,靠墙摆放的梯子,当50°≤α≤70°时(α为梯子与地面所成的角),能够使人安全攀爬.现在有一长为6米的梯子AB,试求能够使人安全攀爬时,梯子的顶端能达到的最大高度AC.
(结果保留两个有效数字,sin70°≈0.94,sin50°≈0.77,cos70°≈0.34,cos50°≈0.64)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)﹣![]() ﹣[(﹣3) ﹣2×
﹣[(﹣3) ﹣2× ![]() ﹣8.5]÷(﹣
﹣8.5]÷(﹣ ![]() )
)
(2)![]() ×
×![]() ﹣0.25×(﹣4)×(﹣3);
﹣0.25×(﹣4)×(﹣3);
(3)(﹣1![]() )﹣1
)﹣1![]() +(﹣
+(﹣ ![]() )﹣3
)﹣3![]() ﹣(﹣1
﹣(﹣1![]() )
)
(4)![]() ÷4
÷4 ![]() ×(﹣
×(﹣![]() )+5﹣2×(﹣
)+5﹣2×(﹣ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有6个红球,9个黄球,3个白球,这些球除颜色外其他均相同.从中任意摸出一个球.
(1)求摸到的球是白球的概率.
(2)如果要使摸到白球的概率为![]() ,需要在这个口袋中再放入多少个白球?
,需要在这个口袋中再放入多少个白球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察发现
![]() ,
,![]() ,
,![]() ,……,
,……,![]() .
.
![]() =1﹣
=1﹣![]() =
=![]() .
.
![]() =1﹣
=1﹣![]() =
=![]() .
.
![]() = .
= .
(2)构建模型
![]() = .(n为正整数)
= .(n为正整数)
(3)拓展应用:
①![]() = .
= .
②![]() = .
= .
③一个数的八分之一,二十四分之一,四十八分之一,八十分之一的和比这个数的四分之一小1,求这个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧 ![]() (不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( )
(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( ) 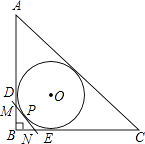
A.r
B.![]() ?r
?r
C.2r
D.![]() ?r
?r
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com