
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据无限不循环小数叫做无理数,判断出在-$\sqrt{(-5)^{2}}$,2π,$\sqrt{0.4}$,$\frac{1}{7}$,0中无理数个数为多少即可.
解答 解:∵-$\sqrt{(-5)^{2}}$=-5,$\frac{1}{7}$=0.$\stackrel{•}{1}$4285$\stackrel{•}{7}$,
∴在-$\sqrt{(-5)^{2}}$,2π,$\sqrt{0.4}$,$\frac{1}{7}$,0中无理数个数为2个:2π,$\sqrt{0.4}$.
故选:B.
点评 此题主要考查了无理数的特征和判断,要熟练掌握,解答此题的关键是要明确:判断一个数是否为无理数,不能只看形式,要看化简结果.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
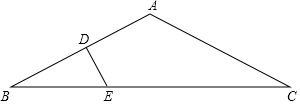 如图,△ABC中,AB=AC=2$\sqrt{5}$,BC=8,AB的垂直平分线交AB于点D,交BC于点E,设△BDE的面积为S1,四边形ADEC的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于$\frac{5}{27}$.
如图,△ABC中,AB=AC=2$\sqrt{5}$,BC=8,AB的垂直平分线交AB于点D,交BC于点E,设△BDE的面积为S1,四边形ADEC的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于$\frac{5}{27}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②⑤ | C. | ①②④ | D. | ②⑤⑥ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>0 | B. | k>1 | C. | k<1 | D. | k≥1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 平均成绩 | 中位数 | |
| 甲 | 10 | 8 | 9 | 8 | 10 | 9 | 9 | ① |
| 乙 | 10 | 7 | 10 | 10 | 9 | 8 | ② | 9.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com