
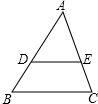
 如图,在△ABC中,DE∥BC,交AB、AC于点D、E,且AD:DB=3:2,若梯形DBCE的面积等于32,则S△ABC=
如图,在△ABC中,DE∥BC,交AB、AC于点D、E,且AD:DB=3:2,若梯形DBCE的面积等于32,则S△ABC=

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
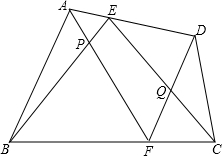 已知在任意四边形ABCD中,点E、F分别将AD、BC分成两部分,AF和BE交于P,CE和DF交于Q,求证:S四边形EPFQ=S△CDQ+S△ABP.
已知在任意四边形ABCD中,点E、F分别将AD、BC分成两部分,AF和BE交于P,CE和DF交于Q,求证:S四边形EPFQ=S△CDQ+S△ABP.查看答案和解析>>
科目:初中数学 来源: 题型:
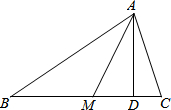 如图,在△ABC中,∠C=60°,AM是△ABC的角平分线,AD是△ABC的高线.
如图,在△ABC中,∠C=60°,AM是△ABC的角平分线,AD是△ABC的高线.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
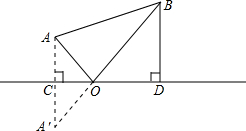 如图,A、B两个村子在河CD的同侧,AB2=13km,A、B两村子到河的距离分别为AC=1km,BD=3km.现在要在河边CD上建一水厂,向A、B村输送自来水,铺设水管的工程费为每千米3000元,请你在CD上选择水厂的位置O,使铺设水管费用的最省,并求出铺设水管的总费用W.
如图,A、B两个村子在河CD的同侧,AB2=13km,A、B两村子到河的距离分别为AC=1km,BD=3km.现在要在河边CD上建一水厂,向A、B村输送自来水,铺设水管的工程费为每千米3000元,请你在CD上选择水厂的位置O,使铺设水管费用的最省,并求出铺设水管的总费用W.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com