
【题目】某旅游风景区出售一种纪念品,该纪念品的成本为![]() 元/个,这种纪念品的销售价格为
元/个,这种纪念品的销售价格为![]() (元/个)与每天的销售数量
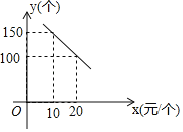
(元/个)与每天的销售数量![]() (个)之间的函数关系如图所示.
(个)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)销售价格定为多少时,每天可以获得最大利润?并求出最大利润.
(3)“十一”期间,游客数量大幅增加,若按八折促销该纪念品,预计每天的销售数量可增加![]() ,为获得最大利润,“十一”假期该纪念品打八折后售价为多少?
,为获得最大利润,“十一”假期该纪念品打八折后售价为多少?
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线![]() 的抛物线
的抛物线![]() 与x轴相交于A、B两点,其中A点的坐标为(-3,0)。
与x轴相交于A、B两点,其中A点的坐标为(-3,0)。

(1)求点B的坐标;
(2)已知![]() ,C为抛物线与y轴的交点。
,C为抛物线与y轴的交点。
①若点P在抛物线上,且![]() ,求点P的坐标;
,求点P的坐标;
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线![]() 的抛物线
的抛物线![]() 与x轴相交于A、B两点,其中A点的坐标为(-3,0)。
与x轴相交于A、B两点,其中A点的坐标为(-3,0)。

(1)求点B的坐标;
(2)已知![]() ,C为抛物线与y轴的交点。
,C为抛物线与y轴的交点。
①若点P在抛物线上,且![]() ,求点P的坐标;
,求点P的坐标;
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
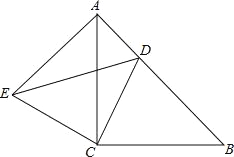
【题目】如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点,
(1)求证:△ACE≌△BCD;
(2)若DE=13,BD=12,求线段AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
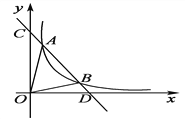
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(m,6),B(3,n)两点.
(x>0)的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出kx+b-![]() <0时x的取值范围;
<0时x的取值范围;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】联想三角形内心的概念,我们可引入如下概念.
定义:到三角形的两边距离相等的点,叫做此三角形的准内心.
举例:如图1,若PD=PE,则点P为△ABC的准内心.
应用:如图2,BF为等边三角形的角平分线,准内心P在BF上,且PF=![]() BP,求证:点P是△ABC的内心.
BP,求证:点P是△ABC的内心.
探究:已知△ABC为直角三角形,∠C=90°,准内心P在AC上,若PC=![]() AP,求∠A的度数.
AP,求∠A的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
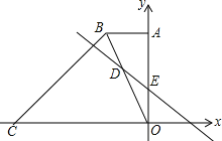
【题目】如图,在平面直角坐标中,直角梯形OABC的边OC、OA分别在x轴、y轴上,AB∥OC,∠AOC=90°,∠BCO=45°,BC=12![]() ,点C的坐标为(-18,0).
,点C的坐标为(-18,0).
(1)求点B的坐标;
(2)若直线DE交梯形对角线BO于点D,交y轴于点E,且OE=4,∠OFE=45°,求直线DE的解析式;
(3)求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高高的路灯挂在路边的上方,高傲而明亮,小明拿着一根2米长的竹竿,想量一量路灯的高度,直接量是不可能的.于是,他走到路灯旁的一个地方,竖起竹竿(即AE),这时,他量了一下竹竿的影长(AC)正好是1米,他沿着影子的方向走,向远处走出两根竹竿的长度(即AB=4米),他又竖起竹竿,这时竹竿的影长正好是一根竹竿的长度(即BD=2米).此时,小明抬头瞧瞧路灯,若有所思地说:“噢,我知道路灯有多高了!”同学们,请你和小明一起解答这个问题:
(1)在图中作出路灯O的位置,并作OP⊥l于P.
(2)求出路灯O的高度,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,点O为坐标原点,经过A(-2,6)的直线交x轴正半轴于点B,交y轴于点C,OB=OC,直线AD交x轴负半轴于点D,若△ABD的面积为27.
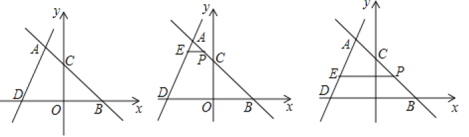
(1)求直线AD的解析式;
(2)横坐标为m的点P在AB上(不与点A,B重合),过点P作x轴的平行线交AD于点E,设PE的长为y(y≠0),求y与m之间的函数关系式并直接写出相应的m的取值范围;
(3)在(2)的条件下,在x轴上是否存在点F,使△PEF为等腰直角三角形?若存在求出点F的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com