
【题目】如图,在平面直角坐标中,直角梯形OABC的边OC、OA分别在x轴、y轴上,AB∥OC,∠AOC=90°,∠BCO=45°,BC=12![]() ,点C的坐标为(-18,0).
,点C的坐标为(-18,0).
(1)求点B的坐标;
(2)若直线DE交梯形对角线BO于点D,交y轴于点E,且OE=4,∠OFE=45°,求直线DE的解析式;
(3)求点D的坐标.
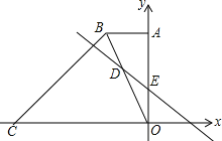
【答案】(1)(-6,12);(2)y=-x+4;(3)D(-4,8)
【解析】
(1)过B作BG⊥x轴,交x轴于点G,由题意得到三角形BCG为等腰直角三角形,根据BC的长求出CG与BG的长,根据OC-CG求出OG的长,确定出B坐标即可;
(2)由题意得到三角形EOF为等腰直角三角形,确定出E与F的坐标,设直线DE解析式为y=kx+b,把E与F代入求出k与b的值,确定出直线DE解析式;
(3)设直线OB解析式为y=mx,把B坐标代入求出m的值,确定出OB解析式,与直线DE解析式联立求出D坐标即可.

解:(1)过B作BG⊥x轴,交x轴于点G,
在Rt△BCG中,∠BCO=45°,BC=12![]() ,
,
∴BG=CG=12,
∵C(﹣18,0),即OC=18,
∴OG=OC-CG=18-12=6,
则B=(﹣6,12);
(2)∵∠EOF=90°,∠OFE=45°,
∴△OEF为等腰直角三角形,
∴OE=OF=4,即E(0,4),F(4,0),
设直线DE解析式为y=kx+b,
把E与F坐标代入得:![]() ,
,
解得:k=﹣1,b=4,
∴直线DE解析式为y=﹣x+4;
(3)设直线OB解析式为y=mx,把B(-6,12)代入得:m=﹣2,
∴直线OB解析式为y=﹣2x,
联立得:![]() ,
,
解得:![]() ,
,
则D(﹣4,8).


科目:初中数学 来源: 题型:
【题目】已知:如图,菱形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,且BE=BF=DH=DG.
(1)求证:四边形EFGH是矩形;
(2)已知∠B=60°,AB=6.
请从A,B两题中任选一题作答,我选择 题.
A题:当点E是AB的中点时,矩形EFGH的面积是 .
B题:当BE= 时,矩形EFGH的面积是8![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO![]() ;⑤S△AOC+S△AOB=
;⑤S△AOC+S△AOB=![]() .其中正确的结论是( )
.其中正确的结论是( )

A.①②③⑤B.①②③④C.①②③④⑤D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
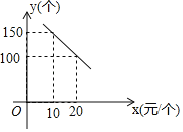
【题目】某旅游风景区出售一种纪念品,该纪念品的成本为![]() 元/个,这种纪念品的销售价格为
元/个,这种纪念品的销售价格为![]() (元/个)与每天的销售数量
(元/个)与每天的销售数量![]() (个)之间的函数关系如图所示.
(个)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)销售价格定为多少时,每天可以获得最大利润?并求出最大利润.
(3)“十一”期间,游客数量大幅增加,若按八折促销该纪念品,预计每天的销售数量可增加![]() ,为获得最大利润,“十一”假期该纪念品打八折后售价为多少?
,为获得最大利润,“十一”假期该纪念品打八折后售价为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线AB与![]() 轴交于点A,与
轴交于点A,与![]() 轴交于点B,与直线OC:
轴交于点B,与直线OC:![]() 交于点C.
交于点C.
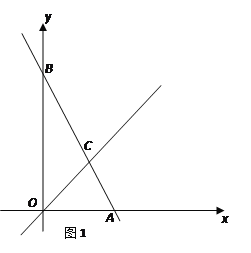

(1)若直线AB解析式为![]() ,
,
①求点C的坐标;
②求△OAC的面积.
(2)如图2,作![]() 的平分线ON,若AB⊥ON,垂足为E, OA=4,P、Q分别为线段OA、OE上的动点,连结AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.
的平分线ON,若AB⊥ON,垂足为E, OA=4,P、Q分别为线段OA、OE上的动点,连结AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.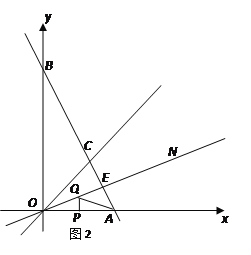
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下面的平面直角坐标系中,画出符合下列条件的点:
(1)画出5个纵坐标比横坐标大2的点,分别标上![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)画出5个横坐标是纵坐标的2倍的点,分别标上![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(3)观察上面两题所画出的点,你有什么发现,分别用语言叙述出来.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了绿化环境,某中学八年级(3班)同学都积极参加了植树活动,下面是今年3月份该班同学植树情况的形统计图和不完整的条形统计图:
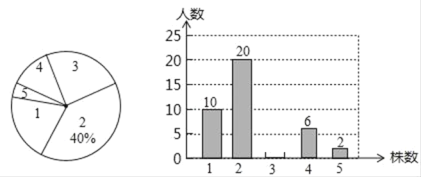
请根据以上统计图中的信息解答下列问题.
(1)植树3株的人数为 ;
(2)该班同学植树株数的中位数是 ;
(3)求该班同学平均植树的株数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年四川泸州8分)如图,为了测出某塔CD的高度,在塔前的平地上选择一点A,用测角仪测得塔顶D的仰角为30°,在A、C之间选择一点B(A、B、C三点在同一直线上).用测角仪测得塔顶D的仰角为75°,且AB间的距离为40m.

(1)求点B到AD的距离;
(2)求塔高CD(结果用根号表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商从市场得知如下信息:
某品牌空调扇 | 某品牌电风扇 | |
进价(元/台) | 700 | 100 |
售价(元/台) | 900 | 160 |
他现有40000元资金可用来一次性购进该品牌空调扇和电风扇共100台,设该经销商购进空调扇![]() 台,空调扇和电风扇全部销售完后获得利润为
台,空调扇和电风扇全部销售完后获得利润为![]() 元.
元.
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)利用函数性质,说明该经销商如何进货可获利最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com