【题目】在北京市治理违建的过程中，某小区拆除了自建房，改建绿地. 如图，自建房占地是边长为8m的正方形ABCD，改建的绿地是矩形AEFG，其中点E在AB上，点G在AD的延长线上，且DG = 2BE. 如果设BE的长为x（单位：m），绿地AEFG的面积为y（单位：m2），那么y与x的函数的表达式为__________________；当BE =______m时，绿地AEFG的面积最大.
科目：初中数学 来源： 题型：
【题目】某学校开展了“好读书、读好书”的课外阅读活动，为了解同学们的读书情况，从全校随机抽取了
名学生，并统计它们平均每天的课外阅读时间（单位：
），然后利用所得数据绘制成如下不完整的统计图表.
课外阅读时间频数分布表
课外阅读时间 | 频数 | 百分比 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
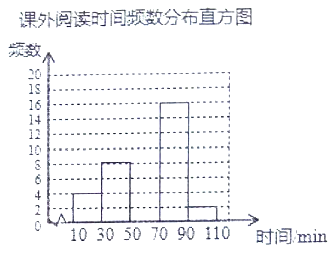
请根据图表中提供的信息回答下列问题：
（1）填空：
__________，
__________；
（2）将频数分布直方图补充完整；
（3）若全校有
名学生，估计该校有多少名学生平均每天的课外阅读时间不少于
？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在正方形ABCD中，E是△ABD内的点，EB=EC．
（1）如图1，若EB=BC，求∠EBD的度数；
（2）如图2，EC与BD交于点F，连接AE，若
，试探究线段FC与BE之间的等量关系，并说明理由．
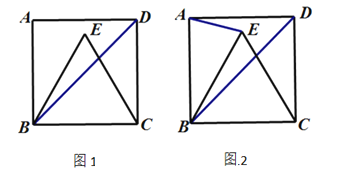
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，坡AB的坡比为1：2.4，坡长AB=130米，坡AB的高为BT．在坡AB的正面有一栋建筑物CH，点H、A、T在同一条地平线MN上．
（1）试问坡AB的高BT为多少米？
（2）若某人在坡AB的坡脚A处和中点D处，观测到建筑物顶部C处的仰角分别为60°和30°，试求建筑物的高度CH．（精确到米， 
≈1.73， 
≈1.41）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】图a是一个长为2m、宽为2n的长方形，沿图中实现用剪刀均分成四块小长方形，然后按图b的形状拼成一个正方形．
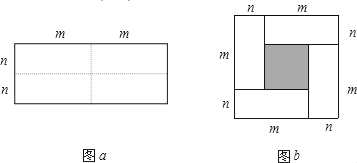
（1）图b中，大正方形的边长是 ．阴影部分小正方形的边长是 ；
（2）观察图b，写出（m+n）2，（m﹣n）2，mn之间的一个等量关系，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为传播奥运知识，小刚就本班学生对奥运知识的了解程度进行了一次调查统计：A：熟悉，B：了解较多，C：一般了解图1和图2是他采集数据后，绘制的两幅不完整的统计图，请你根据图中提供的信息解答以下问题：
（1）求该班共有多少名学生；
（2）在条形图中，将表示“一般了解”的部分补充完整；
（3）在扇形统计图中，计算出“了解较多”部分所对应的圆心角的度数；
（4）如果全年级共1000名同学，请你估算全年级对奥运知识“了解较多”的学生人数.
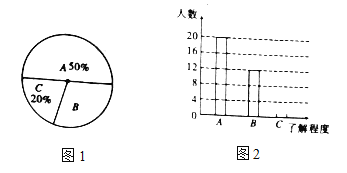
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在前面学习中，一些乘法公式可以通过几何图形来进行验证，请结合下列两组图形回答问题：
图①说明：左侧图形中阴影部分由右侧阴影部分分割后拼接而成.
图②说明：边长为
的正方形的面积分割成如图所示的四部分.
（1）请结合图①和图②分别写出学过的两个乘法公式：
图①：____________，图②：____________；
（2）请利用上面的乘法公式计算：
①
；
②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
