
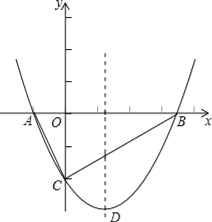
【题目】如图,抛物线y=![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.
【答案】(1)![]() , D (
, D (![]() ,
,![]() );(2)△ABC是直角三角形,证明见解析;
);(2)△ABC是直角三角形,证明见解析;
(3)M(![]() ,0).
,0).
【解析】(1)∵点A(-1,0)在抛物线y=![]() x2 + bx-2上,
x2 + bx-2上,
∴![]() × (-1 )2 + b× (-1)–2 = 0,
× (-1 )2 + b× (-1)–2 = 0,
![]() 解得b =
解得b =![]() ,
,
∴ 抛物线的解析式为y=![]() x2-
x2-![]() x-2.
x-2.
y= ( x2 -3x- 4 ) =![]() (x-)2-
(x-)2-![]() ,
,
∴顶点D的坐标为 (![]() , -
, -![]() ).
).
(2)当x = 0时y = -2,
∴C(0,-2),OC = 2。
当y = 0时, ![]() x2-
x2-![]() x-2 = 0,
x-2 = 0,
∴x1 =-1, x2 = 4,
∴B (4,0)
∴OA = 1, OB = 4, AB = 5.
∵AB2 = 25, AC2 = OA2 + OC2 = 5, BC2 = OC2 + OB2 = 20,
∴AC2 +BC2 = AB2.
∴△ABC是直角三角形.
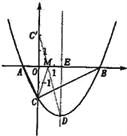
(3)作出点C关于x轴的对称点C′,则C′(0,2),OC′=2,连接C′D交x轴于点M,根据轴对称性及两点之间线段最短可知,MC + MD的值最小及△DCM的周长最小
设抛物线的对称轴交x轴于点E.
∵ED∥y轴, ∴∠OC′M=∠EDM,∠C′OM=∠DEM
∴△C′OM∽△DEM.
∴![]()
∴![]() , ∴m =
, ∴m =![]() .
.
所以M的坐标为(![]() ,0)
,0)


科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,点P(-2,3)关于x轴对称的点的坐标为( )
A. (3,-2) B. (2,-3) C. (-3,2) D. (-2,-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系xOy中,平行四边形ABCD四个顶点的坐标分别为A(1,1),B(4,1),C(5,2),D(2,2),直线l:y=kx+b与直线y=﹣2x平行.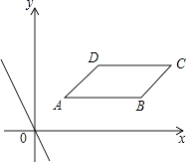

(1)若直线l过点D,求直线l的解析式;
(2)若直线l同时与边AB和CD都相交,求b的取值范围;
(3)若直线l沿线段AC从点A平移至点C,设直线l与x轴的交点为P,问是否存在一点P,使△PAB为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
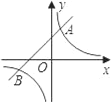
【题目】已知:如图,反比例函数y=![]() 的图象与一次函数y=mx+b的图象交于A(1,3),B(n,﹣1)两点.
的图象与一次函数y=mx+b的图象交于A(1,3),B(n,﹣1)两点.
(1)求反比例函数与一次函数的解析式;
(2)根据图象回答:当x取何值时,反比例函数的值大于一次函数的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
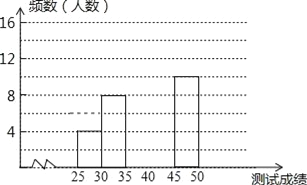
【题目】为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
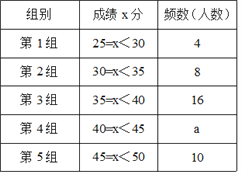
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
(4)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小宇与小强两名男同学能分在同一组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com