
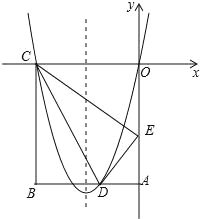
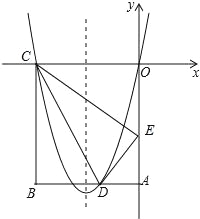
【题目】如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在边OA上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.
(1)求OE的长及经过O,D,C三点抛物线的解析式;
(2)一动点P从点C出发,沿CB以每秒2个单位长度的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长度的速度向点C运动,当点P到达点B时,两点同时停止运动,设运动时间为t秒,当t为何值时,DP=DQ;
(3)若点N在(1)中抛物线的对称轴上,点M在抛物线上,是否存在这样的点M与点N,使M,N,C,E为顶点的四边形是平行四边形?若存在,请求出M点坐标;若不存在,请说明理由.
【答案】(1)在Rt△COE中,OE=![]() =
=![]() =3,抛物线解析式为y=
=3,抛物线解析式为y=![]() x(x+4)=
x(x+4)=![]() x2+
x2+![]() x;
x;
(2)t=![]() ;
;
(3)存在满足条件的点M,其坐标为(2,16)或(﹣6,16)或(﹣2,﹣![]() ).
).
【解析】
试题分析:(1)由折叠的性质可求得CE、CO,在Rt△COE中,由勾股定理可求得OE,设AD=m,在Rt△ADE中,由勾股定理可求得m的值,可求得D点坐标,结合C、O两点,利用待定系数法可求得抛物线解析式;
(2)用t表示出CP、BP的长,可证明△DBP≌△DEQ,可得到BP=EQ,可求得t的值;
(3)可设出N点坐标,分三种情况①EN为对角线,②EM为对角线,③EC为对角线,根据平行四边形的性质可求得对角线的交点横坐标,从而可求得M点的横坐标,再代入抛物线解析式可求得M点的坐标.
试题解析:(1)∵CE=CB=5,CO=AB=4,
∴在Rt△COE中,OE=![]() =
=![]() =3,
=3,
设AD=m,则DE=BD=4﹣m,
∵OE=3,
∴AE=5﹣3=2,
在Rt△ADE中,由勾股定理可得AD2+AE2=DE2,即m2+22=(4﹣m)2,解得m=![]() ,
,
∴D(﹣![]() ,﹣5),
,﹣5),
∵C(﹣4,0),O(0,0),
∴设过O、D、C三点的抛物线为y=ax(x+4),
∴﹣5=﹣![]() a(﹣
a(﹣![]() +4),解得a=
+4),解得a=![]() ,
,
∴抛物线解析式为y=![]() x(x+4)=
x(x+4)=![]() x2+
x2+![]() x;
x;
(2)∵CP=2t,∴BP=5﹣2t,∵BD=![]() ,DE=
,DE=![]() =
=![]() ,∴BD=DE,
,∴BD=DE,
在Rt△DBP和Rt△DEQ中,![]() ,
,
∴Rt△DBP≌Rt△DEQ(HL),
∴BP=EQ,
∴5﹣2t=t,
∴t=![]() ;
;
(3)∵抛物线的对称轴为直线x=﹣2,
∴设N(﹣2,n),
又由题意可知C(﹣4,0),E(0,﹣3),
设M(m,y),
①当EN为对角线,即四边形ECNM是平行四边形时,
则线段EN的中点横坐标为![]() =﹣1,线段CM中点横坐标为
=﹣1,线段CM中点横坐标为![]() ,
,
∵EN,CM互相平分,
∴![]() =﹣1,解得m=2,
=﹣1,解得m=2,
又M点在抛物线上,
∴y=![]() ×22+
×22+![]() ×2=16,
×2=16,
∴M(2,16);
②当EM为对角线,即四边形ECMN是平行四边形时,
则线段EM的中点横坐标为![]() ,线段CN中点横坐标为
,线段CN中点横坐标为![]() =﹣3,
=﹣3,
∵EM,CN互相平分,
∴![]() =﹣3,解得m=﹣6,
=﹣3,解得m=﹣6,
又∵M点在抛物线上,
∴y=![]() ×(﹣6)2+
×(﹣6)2+![]() ×(﹣6)=16,
×(﹣6)=16,
∴M(﹣6,16);
③当CE为对角线,即四边形EMCN是平行四边形时,
则M为抛物线的顶点,即M(﹣2,﹣![]() ).
).
综上可知,存在满足条件的点M,其坐标为(2,16)或(﹣6,16)或(﹣2,﹣![]() ).
).


科目:初中数学 来源: 题型:
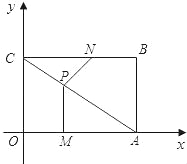
【题目】如图,平面直角坐标系中,四边形OABC为矩形,点A,B的坐标分别为(4,0),(4,3),动点M,N分别从O,B同时出发.以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点M作MP⊥OA,交AC于P,连接NP,已知动点运动了x秒.
(1)P点的坐标为多少(用含x的代数式表示);
(2)试求△NPC面积S的表达式,并求出面积S的最大值及相应的x值;
(3)当x为何值时,△NPC是一个等腰三角形?简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表.现有15升食物需要存放且要求每个盒子要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性返还现金4元,则一次性购买盒子所需要最少费用为 元.
型号 | A | B |
单个盒子容量(升) | 2 | 3 |
单价(元) | 5 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意结合图形填空:已知:如图,AD⊥BC于D,EG⊥BC与G,∠E=∠3,试问:AD是∠BAC的平分线吗?若是,请说明理由.
答:是,理由如下:
∵AD⊥BC,EG⊥BC(已知)
∴∠4=∠5=90°( )
∴AD∥EG( )
∴∠1=∠E( )
∠2=∠3( )
∵∠E=∠3(已知)
∴(∠1)=(∠2)(等量代换)
∴AD是∠BAC的平分线( )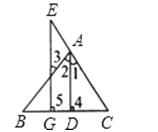
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC≌△DEF,AB=DE,∠A=70°,∠E=30°,则∠F的度数为 ( )
A、 80° B、 70° C、 30 ° D、 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四个命题: ①若一个数的相反数等于它本身,则这个数是0;
②若一个数的倒数等于它本身,则这个数是1;
③若a=b,则a2=b2;
④若一个数的绝对值就等于它本身,则这个数是正数.
其中真命题有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中.
(1)把△ABC平移至A′的位置,使点A与A′对应,得到△A′B′C′;
(2)图中可用字母表示,与线段AA′平行且相等的线段有哪些?
(3)求四边形ACC′A′的面积.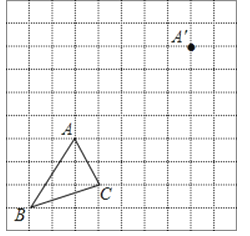
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宁波奥林匹克体育中心坐落于江北区,一期“三馆一圆”总投资35亿元,其中35亿元用科学记数法表示为( )
A.0.35×1010元
B.3.5×108元
C.3.5×109元
D.35×108元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com