
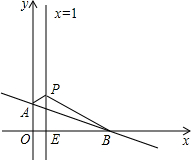
 如图,平面直角坐标系中,直线AB:y=-
如图,平面直角坐标系中,直线AB:y=-| 3 |
| 4 |
| 3 |
| 4 |
| OA2+OM2 |
| 32+22 |
| 13 |
| 22+32 |
| 13 |
| 1 |
| 6 |
| 1 |
| 6 |
| 6 |
| 6 |
| 6 |
| 1 |
| 6 |
| 6 |
| 6 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图,△ABC内接于⊙O,AB为⊙O的直径,∠ACB的平分线CD交⊙O于点D,过点D作⊙O的切线PD,交CA的延长线于点F,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
如图,△ABC内接于⊙O,AB为⊙O的直径,∠ACB的平分线CD交⊙O于点D,过点D作⊙O的切线PD,交CA的延长线于点F,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.| 4 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
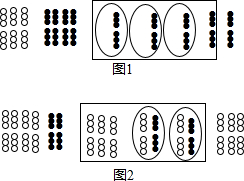 我国是最早认识负数,并进行相关运算的国家.在古代数学名著《九章算术》里,就记载了利用算筹实施“正负术”的方法,图1表示的是计算3+(-4)的过程.按照这种方法,图2表示的过程应是在计算( )
我国是最早认识负数,并进行相关运算的国家.在古代数学名著《九章算术》里,就记载了利用算筹实施“正负术”的方法,图1表示的是计算3+(-4)的过程.按照这种方法,图2表示的过程应是在计算( )| A、(-5)+(-2) |
| B、(-5)+2 |
| C、5+(-2) |
| D、5+2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com