
【题目】如图,在△ABC中,AB=AC,E,F分别是BC,AC的中点,以AC为斜边作Rt△ADC,若∠CAD=∠CAB=45°,则下列结论不正确的是( ) 
A.∠ECD=112.5°
B.DE平分∠FDC
C.∠DEC=30°
D.AB= ![]() CD
CD
【答案】C
【解析】解:∵AB=AC,∠CAB=45°, ∴∠B=∠ACB=67.5°.
∵Rt△ADC中,∠CAD=45°,∠ADC=90°,
∴∠ACD=45°,AD=DC,
∴∠ECD=∠ACB+∠ACD=112.5°,故A正确,不符合题意;
∵E、F分别是BC、AC的中点,
∴FE= ![]() AB,FE∥AB,
AB,FE∥AB,
∴∠EFC=∠BAC=45°,∠FEC=∠B=67.5°.
∵F是AC的中点,∠ADC=90°,AD=DC,
∴FD= ![]() AC,DF⊥AC,∠FDC=45°,
AC,DF⊥AC,∠FDC=45°,
∵AB=AC,
∴FE=FD,
∴∠FDE=∠FED= ![]() (180°﹣∠EFD)=
(180°﹣∠EFD)= ![]() (180°﹣135°)=22.5°,
(180°﹣135°)=22.5°,
∴∠FDE= ![]() ∠FDC,
∠FDC,
∴DE平分∠FDC,故B正确,不符合题意;
∵∠FEC=∠B=67.5°,∠FED=22.5°,
∴∠DEC=∠FEC﹣∠FED=45°,故C错误,符合题意;
∵Rt△ADC中,∠ADC=90°,AD=DC,
∴AC= ![]() CD,
CD,
∵AB=AC,
∴AB= ![]() CD,故D正确,不符合题意.
CD,故D正确,不符合题意.
故选C.
【考点精析】掌握等腰三角形的性质和三角形中位线定理是解答本题的根本,需要知道等腰三角形的两个底角相等(简称:等边对等角);连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数y=(k﹣3)x+2k﹣8
(1)若一次函数的图象经过原点,求k的值;
(2)若一次函数的图象与直线y=2x+1平行,求k的值;
(3)若一次函数y的值随x的值的增大而减小,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两根木棒分别为5cm和7cm,要选择第三根木棒,将它们钉成一个三角形,如果第三根木棒长为偶数,则方法有( )
A.3种B.4种C.5种D.6种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.用一个平面去截一个圆锥,可以是椭圆
B.棱柱的所有侧棱长都相等
C.用一个平面去截一个圆柱体,截面可以是梯形
D.用一个平面去截一个长方体截面不能是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,种植花卉的利润y2与投资量x的平方成正比例关系,并得到了表格中的数据.
投资量x(万元) | 2 |
种植树木利润y1(万元) | 4 |
种植花卉利润y2(万元) | 2 |
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利利润W万元,直接写出W关于m的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?
(3)若该专业户想获利不低于22万,在(2)的条件下,直接写出投资种植花卉的金额m的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
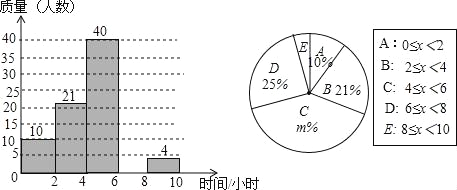
【题目】某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图.根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图;
(2)求扇形统计图中m的值和“E”组对应的圆心角度数;
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com