
【题目】已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长.

【答案】(1)证明见解析;(2)AD=![]() .
.
【解析】试题分析:(1)连接FO,由F为BC的中点,AO=CO,得到OF∥AB,由于AC是⊙O的直径,得出CE⊥AE,根据OF∥AB,得出OF⊥CE,于是得到OF所在直线垂直平分CE,推出FC=FE,OE=OC,再由∠ACB=90°,即可得到结论.
(2)证出△AOE是等边三角形,得到∠EOA=60°,再由直角三角形的性质即可得到结果.
试题解析:(1)如图1,连接FO,
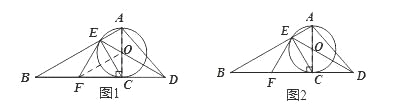
∵F为BC的中点,AO=CO,
∴OF∥AB,
∵AC是⊙O的直径,
∴CE⊥AE,
∵OF∥AB,
∴OF⊥CE,
∴OF所在直线垂直平分CE,
∴FC=FE,OE=OC,
∴∠FEC=∠FCE,∠0EC=∠0CE,
∵∠ACB=90°,
即:∠0CE+∠FCE=90°,
∴∠0EC+∠FEC=90°,
即:∠FEO=90°,
∴FE为⊙O的切线;
(2)如图2,∵⊙O的半径为3,
∴AO=CO=EO=3,
∵∠EAC=60°,OA=OE,
∴∠EOA=60°,
∴∠COD=∠EOA=60°,
∵在Rt△OCD中,∠COD=60°,OC=3,
∴CD=![]() ,
,
∵在Rt△ACD中,∠ACD=90°,
CD=![]() ,AC=6,
,AC=6,
∴AD=![]() .
.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,E,F分别是BC,AC的中点,以AC为斜边作Rt△ADC,若∠CAD=∠CAB=45°,则下列结论不正确的是( ) 
A.∠ECD=112.5°
B.DE平分∠FDC
C.∠DEC=30°
D.AB= ![]() CD
CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为: ;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2![]() ,CD=
,CD=![]() BC,请求出GE的长.
BC,请求出GE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是
是 ![]() 的中线,
的中线, ![]() 是线段
是线段 ![]() 上一点(不与点
上一点(不与点 ![]() 重合).
重合). ![]() 交
交 ![]() 于点
于点 ![]() ,
, ![]() ,连结
,连结 ![]() .
.
(1)如图1,当点 ![]() 与
与 ![]() 重合时,求证:四边形
重合时,求证:四边形 ![]() 是平行四边形;
是平行四边形;
(2)如图2,当点 ![]() 不与
不与 ![]() 重合时,(1)中的结论还成立吗?请说明理由.
重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长 ![]() 交
交 ![]() 于点
于点 ![]() ,若
,若 ![]() ,且
,且 ![]() .
.
①求 ![]() 的度数;
的度数;
②当 ![]() ,
, ![]() 时,求
时,求 ![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列几何体:①球;②长方体;③圆柱;④圆锥;⑤正方体,用一个平面去截上面的几何体,其中能截出圆的几何体有( )
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图.在平面直角坐标系 ![]() 中,直线AB分别与
中,直线AB分别与 ![]() ,
, ![]() 轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥
轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥ ![]() 轴于点E,
轴于点E, ![]() ,OB=4,OE=2.
,OB=4,OE=2.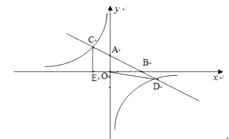
(1)求该反比例函数的解析式;
(2)求△BOD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com