
【题目】△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为: ;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2![]() ,CD=
,CD=![]() BC,请求出GE的长.
BC,请求出GE的长.

【答案】(1)CF⊥BD,BC=CF+CD;(2)成立,证明详见解析;(3)![]() .
.
【解析】试题分析:(1)①根据正方形的性质得到∠BAC=∠DAF=90°,推出△DAB≌△FAC,根据全等三角形的性质即可得到结论;②由正方形ADEF的性质可推出△DAB≌△FAC,根据全等三角形的性质得到CF=BD,∠ACF=∠ABD,根据余角的性质即可得到结论;(2)根据正方形的性质得到∠BAC=∠DAF=90°,推出△DAB≌△FAC,根据全等三角形的性质即可得到结论(3)根据等腰直角三角形的性质得到BC=![]() AB=4,AH=
AB=4,AH=![]() BC=2,求得DH=3,根据正方形的性质得到AD=DE,∠ADE=90°,根据矩形的性质得到NE=CM,EM=CN,由角的性质得到∠ADH=∠DEM,根据全等三角形的性质得到EM=DH=3,DM=AH=2,等量代换得到CN=EM=3,EN=CM=3,根据等腰直角三角形的性质得到CG=BC=4,根据勾股定理即可得到结论.
BC=2,求得DH=3,根据正方形的性质得到AD=DE,∠ADE=90°,根据矩形的性质得到NE=CM,EM=CN,由角的性质得到∠ADH=∠DEM,根据全等三角形的性质得到EM=DH=3,DM=AH=2,等量代换得到CN=EM=3,EN=CM=3,根据等腰直角三角形的性质得到CG=BC=4,根据勾股定理即可得到结论.
试题解析:解:(1)①正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
在△DAB与△FAC中,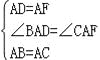 ,
,
∴△DAB≌△FAC,
∴∠B=∠ACF,
∴∠ACB+∠ACF=90°,即CF⊥BD;
②△DAB≌△FAC,
∴CF=BD,
∵BC=BD+CD,
∴BC=CF+CD;
(2)成立,
∵正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
在△DAB与△FAC中, ,
,
∴△DAB≌△FAC,
∴∠B=∠ACF,CF=BD
∴∠ACB+∠ACF=90°,即CF⊥BD;
∵BC=BD+CD,
∴BC=CF+CD;
(3)解:过A作AH⊥BC于H,过E作EM⊥BD于M,EN⊥CF于N,
∵∠BAC=90°,AB=AC,
∴BC=![]() AB=4,AH=
AB=4,AH=![]() BC=2,
BC=2,
∴CD=![]() BC=1,CH=
BC=1,CH=![]() BC=2,
BC=2,
∴DH=3,
由(2)证得BC⊥CF,CF=BD=5,
∵四边形ADEF是正方形,
∴AD=DE,∠ADE=90°,
∵BC⊥CF,EM⊥BD,EN⊥CF,
∴四边形CMEN是矩形,
∴NE=CM,EM=CN,
∵∠AHD=∠ADC=∠EMD=90°,
∴∠ADH+∠EDM=∠EDM+∠DEM=90°,
∴∠ADH=∠DEM,
在△ADH与△DEM中,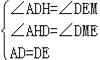 ,
,
∴△ADH≌△DEM,
∴EM=DH=3,DM=AH=2,
∴CN=EM=3,EN=CM=3,
∵∠ABC=45°,
∴∠BGC=45°,
∴△BCG是等腰直角三角形,
∴CG=BC=4,
∴GN=1,
∴EG=![]() =
=![]() .
.



科目:初中数学 来源: 题型:
【题目】如果多项式x+1与x2﹣bx+c的乘积中既不含x2项,也不含x项,则b、c的值是( )
A.b=c=1
B.b=c=﹣1
C.b=c=0
D.b=0,c=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一工厂要将100吨货物运往外地,计划租用某运输公司甲、乙两种型号的汽车共6辆一次将货物全部运动,已知每辆甲型汽车最多能装该种货物16吨,租金800元,每辆乙型汽车最多能装该种货物18吨,租金850元,若此工厂计划此次租车费用不超过5000元,通过计算求出该公司共有几种租车方案?请你设计出来,并求出最低的租车费用。
查看答案和解析>>
科目:初中数学 来源: 题型:
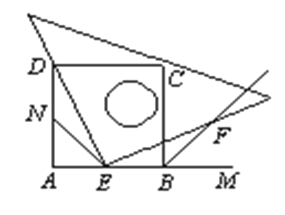
【题目】如图所示,四边形ABCD是正方形,M是AB延长线上一点。直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F。
⑴如图1,当点E在AB边的中点位置时:
①通过测量DE,EF的长度,猜想DE与EF满足的数量关系是 ;
②连接点E与AD边的中点N,猜想NE与BF满足的数量关系是 ;
⑵请你证明上述两种猜想?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,那么该商店有哪几种购买方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com