【题目】一工厂要将100吨货物运往外地，计划租用某运输公司甲、乙两种型号的汽车共6辆一次将货物全部运动，已知每辆甲型汽车最多能装该种货物16吨，租金800元，每辆乙型汽车最多能装该种货物18吨，租金850元，若此工厂计划此次租车费用不超过5000元，通过计算求出该公司共有几种租车方案？请你设计出来，并求出最低的租车费用。
科目：初中数学 来源： 题型：
【题目】特值验证：
当
，0，1，2，5，…时，计算代数式
的值，分别得到5，2，1，2，17，…．当x的取值发生变化时，代数式的值却有一个确定的范围，通过多次验证可以发现它的值总大于或等于1，所以1就是它的最小值．
变式求证：
我们可以用学过的知识，对进行恒等变形：
．（注：这种变形方法可称为“配方”） 
，
．所以无论x取何值，代数式的值不小于1，即最小值为1．
迁移实证：
（1）请你用“配方”的方法，确定
的最小值为3；
（2）求
的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B，C重合），以AD为边在AD右侧作正方形ADEF，连接CF．
（1）观察猜想
如图1，当点D在线段BC上时，
①BC与CF的位置关系为： ．
②BC，CD，CF之间的数量关系为： ；（将结论直接写在横线上）
（2）数学思考
如图2，当点D在线段CB的延长线上时，结论①，②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．
（3）拓展延伸
如图3，当点D在线段BC的延长线上时，延长BA交CF于点G，连接GE．若已知AB=2
，CD=
BC，请求出GE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】请把下列的证明过程补充完整：
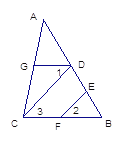
如图，已知∠AGD＝∠ACB，∠1＝∠2。求证：CD∥EF。（填空并在后面的括号中填理由）
证明：∵∠AGD＝∠ACB（ ）
∴DG∥ （ ）
∴∠3＝ （ ）
∵∠1＝∠2 （ ）
∴∠3＝ （等量代换）
∴ ∥ （ ）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
