
【题目】如图,在![]() 中,
中, ![]() ,点
,点![]() 分别是
分别是![]() 的中点,
的中点, ![]() 是
是![]() 延长线上的一点,且
延长线上的一点,且![]() .
.
(1)求证: ![]() ;
;
(2)求证: ![]() .
.

【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据三角形中位线定理可得DE=![]() BC,再根据
BC,再根据![]() ,从而可得DE=CF;
,从而可得DE=CF;
(2)利用SAS证明△BDE≌△ECF即可得.
试题解析:(1)∵点![]() 分别是
分别是![]() 的中点,
的中点,
∴DE‖BC,且DE=![]() BC,
BC,
∵![]() ,∴DE=CF;
,∴DE=CF;
(2)∵AD=BD=![]() AB,AE=EC=
AB,AE=EC=![]() AC,AB=AC,
AC,AB=AC,
∴BD=EC, AD=AE,
∴∠ADE=∠AED,
∴∠BDE=180°-∠ADE=180°-∠AED,
∵DE‖BC,∴∠AED=∠ACB,
∴∠ECF=180°-∠ACB ,∴∠BDE=∠ECF,
又由(1)得DE=CF, ∴△BDE≌△ECF(SAS),
∴BE=EF.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.
的图象与性质.
小亮根据学习函数的经验,对函数![]() 的图象与性质进行了探究。
的图象与性质进行了探究。
下面是小亮的探究过程,请补充完整:
(1)函数![]() 中自变量x的取值范围是_________.
中自变量x的取值范围是_________.
(2)下表是y与x的几组对应值.
x | … | -3 | -2 | -1 | 0 |
|
| 2 | 3 | 4 | 5 | … |
y | … | - | - | -4 | -5 | -7 | m | -1 | -2 | - | - | … |
求m的值;
(3)在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)根据画出的函数图象,发现下列特征:该函数的图象与直线x=1越来越靠近而永不相交,该函数的图象还与直线_________越来越靠近而永不相交.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G,若EF=EG,则CD的长为( )
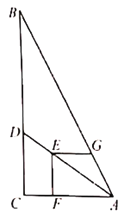
A.3.6B.4C.4.8D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P从![]() 出发,沿所示方向运动,每当碰到长方形OABC的边时会进行反弹,反弹时反射角等于入射角,当点P第2018次碰到长方形的边时,点P的坐标为______.
出发,沿所示方向运动,每当碰到长方形OABC的边时会进行反弹,反弹时反射角等于入射角,当点P第2018次碰到长方形的边时,点P的坐标为______.

【答案】![]()
【解析】
根据反射角与入射角的定义作出图形;由图可知,每6次反弹为一个循环组依次循环,用2018除以6,根据商和余数的情况确定所对应的点的坐标即可.
解:如图所示:经过6次反弹后动点回到出发点![]() ,
,
![]() ,
,
![]() 当点P第2018次碰到矩形的边时为第337个循环组的第2次反弹,
当点P第2018次碰到矩形的边时为第337个循环组的第2次反弹,
![]() 点P的坐标为
点P的坐标为![]() .
.
故答案为:![]() .
.
【点睛】
此题主要考查了点的坐标的规律,作出图形,观察出每6次反弹为一个循环组依次循环是解题的关键.
【题型】填空题
【结束】
15
【题目】为了保护环境,某公交公司决定购买A、B两种型号的全新混合动力公交车共10辆,其中A种型号每辆价格为a万元,每年节省油量为![]() 万升;B种型号每辆价格为b万元,每年节省油量为
万升;B种型号每辆价格为b万元,每年节省油量为![]() 万升:经调查,购买一辆A型车比购买一辆B型车多20万元,购买2辆A型车比购买3辆B型车少60万元.
万升:经调查,购买一辆A型车比购买一辆B型车多20万元,购买2辆A型车比购买3辆B型车少60万元.
![]() 请求出a和b;
请求出a和b;
![]() 若购买这批混合动力公交车每年能节省
若购买这批混合动力公交车每年能节省![]() 万升汽油,求购买这批混合动力公交车需要多少万元?
万升汽油,求购买这批混合动力公交车需要多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“*”定义一种新运算:对于任意有理数a和b,规定a*b=ab2+2ab+a.
如:1*3=1×32+2×1×3+1=16
(1)求2*(﹣2)的值;
(2)若2*x=m,![]() (其中x为有理数),试比较m,n的大小;
(其中x为有理数),试比较m,n的大小;
(3)若[![]() ]
]![]() =a+4,求a的值.
=a+4,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某果品超市经销一种水果,已知该水果的进价为每千克15元,通过一段时间的销售情况发现,该种水果每周的销售总额相同,且每周的销售量y(千克)与每千克售价x(元)的关系如表所示
每千克售价x(元) | 25 | 30 | 40 |
每周销售量y(千克) | 240 | 200 | 150 |
(1)写出每周销售量y(千克)与每千克售价x(元)的函数关系式;
(2)由于销售淡季即将来临,超市要完成每周销售量不低于300千克的任务,则该种水果每千克售价最多定为多少元?
(3)在(2)的基础上,超市销售该种水果能否到达每周获利1200元?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
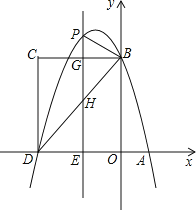
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解决问题:
截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用.具体的做法是在某条线段上截取一条线段等于某特定线段,或将某条线段延长,使之与某特定线段相等,再利用全等三角形的性质等有关知识来解决数学问题.
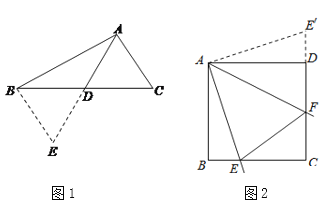
如图1,在△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE,把AB、AC、2AD集中在△ABE中.利用三角形三边的关系即可得4<AE<20 ,则2<AD<10.
(1)问题解决:受到上题解法的启发,如图2,在正方形ABCD中,已知:∠EAF=45°,角的两边AE、AF分别与BC、CD相交于点E、F,若BE=2,DF=3,求EF的长.可延长 CD到E′,使得DE′=BE,连接AE′,先证△ABE≌△ADE′,进一步证明 △AEF≌△AE′F , 即可得EF=E′F, 那么EF=_________.
(2)问题拓展:
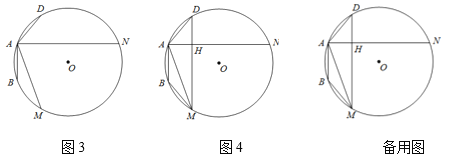
如图3,在⊙O中,AB、AD是⊙O的弦,且AB=AD,M、N是⊙O上的两点,∠MAN=![]() ∠BAD.
∠BAD.
①如图4,连接MN、MD,求证:MH=BM+DH,DM⊥AN;
②若点C在![]() (点C不与点A、D、N重合)上,连接CB、CD分别交AM、AN或其延长线于点E、F,直接写出EF、BE、DF之间的等式关系.
(点C不与点A、D、N重合)上,连接CB、CD分别交AM、AN或其延长线于点E、F,直接写出EF、BE、DF之间的等式关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校随机抽取部分学生,就“学习习惯”进行调查,将“对自己做错题进行整理、分析、改正”(选项为:很少、有时、常常、总是)的调查数据进行了整理,绘制成部分统计图如下:

请根据图中信息,解答下列问题:
(1)该调查的样本容量为________, ![]() =________%,
=________%, ![]() =________%,“常常”对应扇形的圆心角的度数为__________;
=________%,“常常”对应扇形的圆心角的度数为__________;
(2)请你补全条形统计图;
(3)若该校有3200名学生,请你估计其中“总是”对错题进行整理、分析、改正的
学生有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com