
ЁОЬтФПЁПдФЖСЯТСаВФСЯЃЌШЛКѓНтОіЮЪЬтЃК
НиГЄЗЈгыВЙЖЬЗЈдкжЄУїЯпЖЮЕФКЭЁЂВюЁЂБЖЁЂЗжЕШЮЪЬтжагазХЙуЗКЕФгІгУЃЎОпЬхЕФзіЗЈЪЧдкФГЬѕЯпЖЮЩЯНиШЁвЛЬѕЯпЖЮЕШгкФГЬиЖЈЯпЖЮЃЌЛђНЋФГЬѕЯпЖЮбгГЄЃЌЪЙжЎгыФГЬиЖЈЯпЖЮЯрЕШЃЌдйРћгУШЋЕШШ§НЧаЮЕФаджЪЕШгаЙижЊЪЖРДНтОіЪ§бЇЮЪЬтЃЎ
ШчЭМ1ЃЌдкЁїABCжаЃЌШєABЃН12ЃЌACЃН8ЃЌЧѓBCБпЩЯЕФжаЯпADЕФШЁжЕЗЖЮЇЃЎ
НтОіДЫЮЪЬтПЩвдгУШчЯТЗНЗЈЃКбгГЄADЕНЕуEЪЙDEЃНADЃЌдйСЌНгBEЃЌАбABЁЂACЁЂ2ADМЏжадкЁїABEжаЃЎРћгУШ§НЧаЮШ§БпЕФЙиЯЕМДПЩЕУ4<ЃСЃХ<20 ЃЌдђ2<AD<10.
ЃЈ1ЃЉЮЪЬтНтОіЃКЪмЕНЩЯЬтНтЗЈЕФЦєЗЂЃЌШчЭМ2ЃЌдке§ЗНаЮABCDжаЃЌвбжЊЃКЁЯEAF=45ЁуЃЌНЧЕФСНБпAEЁЂAFЗжБ№гыBCЁЂCDЯрНЛгкЕуEЁЂFЃЌШєBE=2ЃЌDF=3ЃЌЧѓEFЕФГЄ.ПЩбгГЄ CDЕНEЁфЃЌЪЙЕУDEЁфЃНBEЃЌСЌНгAEЁфЃЌЯШжЄЁїABEЁеЁїADEЁфЃЌНјвЛВНжЄУї ЁїAEFЁеЁїAEЁфF , МДПЩЕУEF=EЁфF, ФЧУДEF=_________.
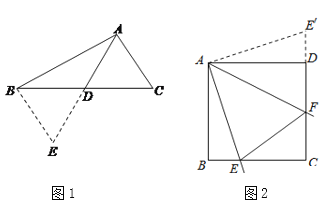
ЃЈ2ЃЉЮЪЬтЭиеЙЃК
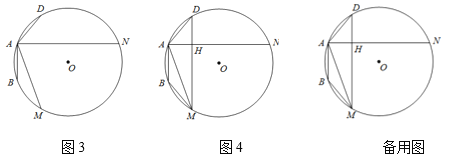
ШчЭМ3ЃЌдкЁбOжаЃЌABЁЂADЪЧЁбOЕФЯвЃЌЧвAB=ADЃЌMЁЂNЪЧЁбOЩЯЕФСНЕуЃЌЁЯMANЃН![]() ЁЯBAD.
ЁЯBAD.
ЂйШчЭМ4ЃЌСЌНгMNЁЂMDЃЌЧѓжЄЃКMH=BM+DHЃЌDMЁЭANЃЛ
ЂкШєЕуCдк![]() ЃЈЕуCВЛгыЕуAЁЂDЁЂNжиКЯЃЉЩЯЃЌСЌНгCBЁЂCDЗжБ№НЛAMЁЂANЛђЦфбгГЄЯпгкЕуEЁЂFЃЌжБНгаДГіEFЁЂBEЁЂDFжЎМфЕФЕШЪНЙиЯЕ.
ЃЈЕуCВЛгыЕуAЁЂDЁЂNжиКЯЃЉЩЯЃЌСЌНгCBЁЂCDЗжБ№НЛAMЁЂANЛђЦфбгГЄЯпгкЕуEЁЂFЃЌжБНгаДГіEFЁЂBEЁЂDFжЎМфЕФЕШЪНЙиЯЕ.
ЁОД№АИЁПЃЈ1ЃЉ5ЃЛЃЈ2ЃЉЂйМћНтЮіЃЌЂкEFЃНBE+DFЛђDFЃНEF+BE
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтФПИјЖЈЕФЫМТЗНјааЧѓНтМДПЩЃЛ
ЃЈ2ЃЉЂйбгГЄMDЕНЕуMЁфЃЌЪЙЕУDMЁф=BMЃЌСЌНгAMЁфЃЌШчЭМ5ЃЎЗТееВФСЯжаЕФжЄУїЫМТЗПЩжЄЕНAM=AMЁфЃЌЁЯMAN=ЁЯMЁфANЃЌШЛКѓРћгУЕШбќШ§НЧаЮЕФаджЪМДПЩНтОіЮЪЬтЃЎЂкЗжСНжжЧщПіЬжТлЃКЂёЃЎЕБЕуCдк![]() ЩЯЪБЃЌШчЭМ1ЁЂ2ЃЛЂђЃЎЕБЕуCдк
ЩЯЪБЃЌШчЭМ1ЁЂ2ЃЛЂђЃЎЕБЕуCдк![]() ЩЯЪБЃЌШчЭМ3ЃЎНшМјЂйжаЕФжЄУїЫМТЗОЭПЩЕУЕННсТлЃЎ
ЩЯЪБЃЌШчЭМ3ЃЎНшМјЂйжаЕФжЄУїЫМТЗОЭПЩЕУЕННсТлЃЎ
ЃЈ1ЃЉбгГЄ CDЕНEЁфЃЌЪЙЕУDEЁфЃНBEЃЌСЌНгAEЁфЃЌ
ЁпЫФБпаЮABCDЪЧе§ЗНаЮЃЌ
ЁрAB=AB,ЁЯB=ЁЯADC=90ЁуЃЌ
ЁрЁЯAD EЁф=90ЁуЃЌ
ЁпDEЁфЃНBEЃЌ
ЁрЁїABEЁеЁїADEЁфЃЌ
ЁрAEЁф=AEЃЌЁЯBAE=ЁЯDA EЁф
ЁрЁЯEЁфAE=90Ёу,
ЁпЁЯEAF=45ЁуЃЌ
ЁрЁЯEЁфAF=45ЁуЃЌ
ЁрЁЯEЁфAF=ЁЯEAF,
дкЁїAEFКЭЁїAEЁфFжаЃЌ
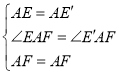 ЃЌ
ЃЌ
Ёр EF=EЁфFЃЌ
ЁпEЁфF=DEЁф+DF=BE+DF=2+3=5,
ЁрEF=5.
ЃЈ2ЃЉЂйбгГЄMDЕНЕуMЁфЃЌЪЙЕУDMЁф=BMЃЌСЌНгAMЁфЃЌШчЭМ5ЃЎ
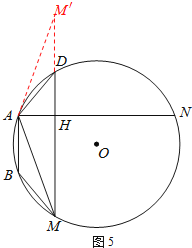
ЁпЁЯADMЁф+ЁЯADM=180ЁуЃЌЁЯABM+ЁЯADM=180ЁуЃЌ
ЁрЁЯABM=ЁЯADMЁфЃЎ
дкЁїABMКЭЁїADMЁфжаЃЌ
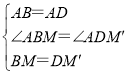 ЃЎ
ЃЎ
ЁрЁїABMЁеЁїADMЁфЃЈSASЃЉЃЎ
ЁрAM=AMЁфЁЯBAM=ЁЯDAMЁфЃЎ
ЁрЁЯMAMЁф=ЁЯBADЃЎ
ЁпЁЯMAN=![]() ЁЯBADЃЌ
ЁЯBADЃЌ
ЁрЁЯMAN=![]() ЁЯMAMЁфЃЎ
ЁЯMAMЁфЃЎ
ЁрЁЯMAN=ЁЯMЁфANЃЎ
ЁпAM=AMЁфЃЌЁЯMAN=ЁЯMЁфANЃЌ
ЁрMH=MЁфHЃЌAHЁЭMMЁфЃЎ
ЁрMH=MЁфH=DMЁф+DH=BM+DHЃЌDMЁЭANЃЎ
ЂкЂкЂёЃЎЕБЕуCдк![]() ЩЯЪБЃЌШчЭМ1ЁЂ2ЃЎ
ЩЯЪБЃЌШчЭМ1ЁЂ2ЃЎ
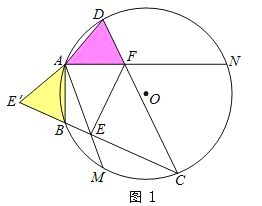
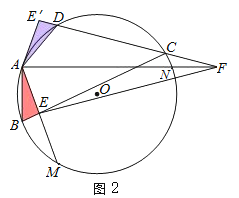
ЭЌРэПЩЕУЃКEF=BE+DFЃЎ
ЂђЃЎЕБЕуCдк![]() ЩЯЪБЃЌШчЭМ3ЃЎ
ЩЯЪБЃЌШчЭМ3ЃЎ
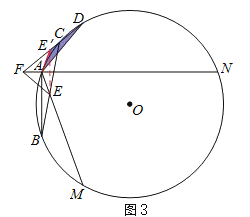
ЭЌРэПЩЕУЃКDFЃНEF+BE.ЃЎ


 ПЊаФЭмзДдЊВтЪдОэЯЕСаД№АИ
ПЊаФЭмзДдЊВтЪдОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ ![]() ЃЌЕу
ЃЌЕу![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ ![]() ЪЧ
ЪЧ![]() бгГЄЯпЩЯЕФвЛЕуЃЌЧв
бгГЄЯпЩЯЕФвЛЕуЃЌЧв![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓжЄЃК ![]() ЃЎ
ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪ§жсЩЯAЁЂBЁЂCШ§ЕуЖдгІЕФЪ§ЗжБ№ЪЧaЁЂbЁЂ7,Тњзу![]() ,
,![]() ,PЮЊЪ§жсЩЯвЛЖЏЕу,ЕуPДгAГіЗЂ,биЪ§жсе§ЗНЯђвдУПУы
,PЮЊЪ§жсЩЯвЛЖЏЕу,ЕуPДгAГіЗЂ,биЪ§жсе§ЗНЯђвдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШдШЫйдЫЖЏ,ЕуQДгЕуCГіЗЂдкЩфЯпCAЩЯЯђЕуAдШЫйдЫЖЏ,ЧвPЁЂQСНЕуЭЌЪБГіЗЂЃЎ
ИіЕЅЮЛГЄЖШЕФЫйЖШдШЫйдЫЖЏ,ЕуQДгЕуCГіЗЂдкЩфЯпCAЩЯЯђЕуAдШЫйдЫЖЏ,ЧвPЁЂQСНЕуЭЌЪБГіЗЂЃЎ

ЃЈ1ЃЉЧѓaЁЂbЕФжЕ
ЃЈ2ЃЉЕБPдЫЖЏЕНЯпЖЮOBЕФжаЕуЪБ,ЕуQдЫЖЏЕФЮЛжУЧЁКУЪЧЯпЖЮABППНќЕуBЕФШ§ЕШЗжЕу,ЧѓЕуQЕФдЫЖЏЫйЖШ
ЃЈ3ЃЉдк![]() ЕФЬѕМўЯТ,ЕБPЁЂQСНЕуМфЕФОрРыЪЧ6ИіЕЅЮЛГЄЖШЪБ,ЧѓOPЕФГЄЃЎ
ЕФЬѕМўЯТ,ЕБPЁЂQСНЕуМфЕФОрРыЪЧ6ИіЕЅЮЛГЄЖШЪБ,ЧѓOPЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯпlЩЯгавЛЕуOЃЌЕуAЁЂBЭЌЪБДгOГіЗЂЃЌдкжБЯпlЩЯЗжБ№ЯђзѓЁЂЯђгвзїдШЫйдЫЖЏЃЌЧвAЁЂBЕФЫйЖШБШЮЊ1ЃК2ЃЌЩшдЫЖЏЪБМфЮЊtsЃЎ

ЃЈ1ЃЉЕБt=2sЪБЃЌAB=12cmЃЎДЫЪБЃЌ
ЂйдкжБЯпlЩЯЛГіAЁЂBСНЕудЫЖЏ2УыЪБЕФЮЛжУЃЌВЂЛиД№ЕуAдЫЖЏЕФЫйЖШЪЧ cm/sЃЛ ЕуBдЫЖЏЕФЫйЖШЪЧ cm/sЃЎ
ЂкШєЕуPЮЊжБЯпlЩЯвЛЕуЃЌЧвPAЉPB=OPЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌШєAЁЂBЭЌЪБАДдЫйЯђзѓдЫЖЏЃЌдйОЙ§МИУыЃЌOA=2OBЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЧѓжЊжабЇгавЛПщЫФБпаЮЕФПеЕиABCDЃЌШчЯТЭМЫљЪОЃЌбЇаЃМЦЛЎдкПеЕиЩЯжжжВВнЦЄЃЌОВтСПЁЯA=90ЁуЃЌAB=3mЃЌBC=12mЃЌCD=13mЃЌDA=4mЃЌШєУПЦНЗНУзВнЦЄашвЊ250дЊЃЌЮЪбЇаЃашвЊЭЖШыЖрЩйзЪН№ТђВнЦЄЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГОАЧјЕФУХЦБЯњЪлЗжСНРрЃКвЛРрЮЊЩЂПЭУХЦБЃЌМлИёЮЊ![]() дЊ/еХЃЛСэвЛРрЮЊЭХЬхУХЦБЃЈвЛДЮадЙКТђУХЦБ
дЊ/еХЃЛСэвЛРрЮЊЭХЬхУХЦБЃЈвЛДЮадЙКТђУХЦБ![]() еХвдЩЯЃЉЃЌУПеХУХЦБМлИёдкЩЂПЭУХЦБМлИёЕФЛљДЁЩЯДђ
еХвдЩЯЃЉЃЌУПеХУХЦБМлИёдкЩЂПЭУХЦБМлИёЕФЛљДЁЩЯДђ![]() елЃЌФГАрВПЗжЭЌбЇвЊШЅИУОАЕуТУгЮЃЌЩшВЮМгТУгЮ
елЃЌФГАрВПЗжЭЌбЇвЊШЅИУОАЕуТУгЮЃЌЩшВЮМгТУгЮ![]() ШЫЃЌЙКТђУХЦБашвЊ
ШЫЃЌЙКТђУХЦБашвЊ![]() дЊ
дЊ
ЃЈ1ЃЉШчЙћУПШЫЗжБ№ТђЦБЃЌЧѓ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃК
жЎМфЕФКЏЪ§ЙиЯЕЪНЃК
ЃЈ2ЃЉШчЙћЙКТђЭХЬхЦБЃЌЧѓ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПЕФШЁжЕЗЖЮЇЃЛ
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЧыИљОнШЫЪ§БфЛЏЩшМЦвЛжжБШНЯЪЁЧЎЕФЙКЦБЗНЪН.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбЇаЃНЬбЇТЅЃЈМзТЅЃЉЕФЖЅВПEКЭДѓУХAжЎМфЙвСЫвЛаЉВЪЦьЃЎаЁгБВтЕУДѓУХAОрМзТЅЕФОрРыABЪЧ31cmЃЌдкAДІВтЕУМзТЅЖЅВПEДІЕФбіНЧЪЧ31ЁуЃЎ
ЃЈ1ЃЉЧѓМзТЅЕФИпЖШМАВЪЦьЕФГЄЖШЃЛЃЈОЋШЗЕН0.01mЃЉ
ЃЈ2ЃЉШєаЁгБдкМзТЅТЅЕзCДІВтЕУбЇаЃКѓУцвНдКТЅЃЈввТЅЃЉТЅЖЅGДІЕФбіНЧЮЊ40ЁуЃЌХРЕНМзТЅТЅЖЅFДІВтЕУввТЅТЅЖЅGДІЕФбіНЧЮЊ19ЁуЃЌЧѓввТЅЕФИпЖШМАМзввСНТЅжЎМфЕФОрРыЃЎЃЈОЋШЗЕН0.01mЃЉ
ЃЈcos31ЁуЁж0.86ЃЌtan31ЁуЁж0.60ЃЌcos19ЁуЁж0.95ЃЌtan19ЁуЁж0.34ЃЌcos40ЁуЁж0.77ЃЌtan40ЁуЁж0.84ЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЕШбќжБНЧШ§НЧаЮABCжаЃЌ![]() DЪЧABЕФжаЕуЃЌEЃЌFЗжБ№ЪЧACЃЌBC.ЩЯЕФЕу(ЕуEВЛгыЖЫЕуAЃЌCжиКЯ)ЃЌЧв
DЪЧABЕФжаЕуЃЌEЃЌFЗжБ№ЪЧACЃЌBC.ЩЯЕФЕу(ЕуEВЛгыЖЫЕуAЃЌCжиКЯ)ЃЌЧв![]() СЌНгEFВЂШЁEFЕФжаЕуOЃЌСЌНгDOВЂбгГЄжСЕуGЃЌЪЙ
СЌНгEFВЂШЁEFЕФжаЕуOЃЌСЌНгDOВЂбгГЄжСЕуGЃЌЪЙ![]() ЃЌСЌНгDEЃЌDFЃЌGEЃЌGF
ЃЌСЌНгDEЃЌDFЃЌGEЃЌGF

(1)ЧѓжЄ:ЫФБпаЮEDFGЪЧе§ЗНаЮ;
(2)жБНгаДГіЕБЕуEдкЪВУДЮЛжУЪБЃЌЫФБпаЮEDFGЕФУцЛ§зюаЁ?зюаЁжЕЪЧЖрЩй?
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com