
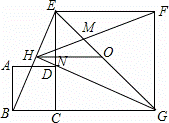
如图,正方形ABCD的边CD在正方形ECGF的边CE上,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接OH,FH,EG与FH交于点M,对于下面四个结论:①CH⊥BE;②HO
 BG;③S正方形ABCD:S正方形ECGF=1:
BG;③S正方形ABCD:S正方形ECGF=1: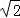 ;④EM:MG=1:(1+
;④EM:MG=1:(1+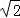 ),其中正确结论的序号为 .
),其中正确结论的序号为 .
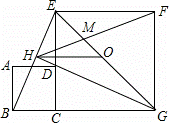
②解:∵四边形ABCD是正方形,
∴BC=DC,∠BCE=90°,
同理可得CE=CG,∠DCG=90°,
在△BCE和△DCG中,
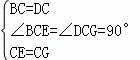 ,
,
∴△BCE≌△DCG,
∴∠BEC=∠DGC,
∵∠EDH=∠ CDG,∠DGC+∠CDG=90°,
CDG,∠DGC+∠CDG=90°,
∴∠EDH+∠BEC=90°,
∴∠EHD=90°,
∴HG⊥BE,则CH⊥BE错误,
则故①错误;
∵在△BGH和△EGH中,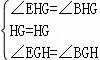 ,
,
∴△BGH≌△EGH,
∴BH=EH,
又∵O是EG的中点,
∴HO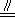
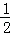 BG,
BG,
故②正确;
设EC和OH相交于点N.
设HN=a,则BC=2a,设正方形ECGF的边长是2b,则NC=b,CD=2a,
∵OH∥BC,
∴△DHN∽△DGC,
∴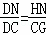 ,即
,即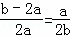 ,即a2+2ab﹣b2=0,
,即a2+2ab﹣b2=0,
解得:a=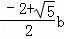 或a=
或a=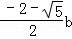 (舍去),
(舍去),
则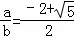 ,
,
则S正方形ABCD:S正方形ECGF=(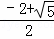 )2=
)2=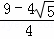 ,故③错误;
,故③错误;
∵EF∥OH,
∴△EFM∽△OMH,
∴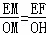 =
=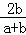 ,
,
∴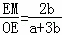 ,
,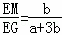
∴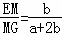 =
=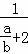 =
=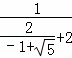 =
=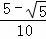 .故④错误.
.故④错误.
故正确的是②.
故答案是:②.


科目:初中数学 来源: 题型:
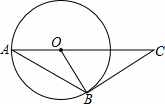
如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=20°,则∠C的度数是( )
|
| A. | 70° | B. | 50° | C. | 45° | D. | 20° |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y= 与正方形ABCD有公共点,则k的取值范围为( )
与正方形ABCD有公共点,则k的取值范围为( )
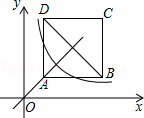
|
| A. | 1<k<9 | B. | 2≤k≤34 | C. | 1≤k≤16 | D. | 4≤k<16 |
查看答案和解析>>
科目:初中数学 来源: 题型:
为了掌握我市中考模拟数学试题的命题质量与难度系数,命题教师赴我市某地选取一个水平相当的初三年级进行调研,命题教师将随机抽取的部分学生成绩(得分为整数,满分为160分)分为5组:第一组85~10;第二组100~115;第三组115~130;第四组130~145;第五组145~160,统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图,观察图形的信息,回答下列问题:
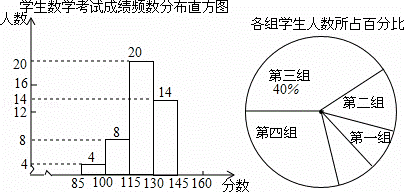
(1)本次调查共随机抽取了该年级多少名学生?并将频数分布直方图补充完整;
(2)若将得分转化为等级,规定:得分低于100分评为“D”,100~130分评为“C”,130~145分评为“B”,145~160分评为“A”,那么该年级1500名考生中,考试成绩评为“B”的学生大约有多少名?
(3)如果第一组只有一名是女生,第五组只有一名是男生,针对考试成绩情况,命题教师决定从第一组、第五组分别随机选出一名同学谈谈做题的感想,请你用列表或画树状图的方法求出所选两名学生刚好是一名女生和一名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
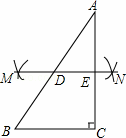
已知在Rt△ABC中,∠ACB=90°,现按如下步骤作图:
①分别以A,C为圆心,a为半径(a> AC)作弧,两弧分别交于M,N两点;
AC)作弧,两弧分别交于M,N两点;
②过M,N两点作直线MN交AB于点D,交AC于点E;
③将△ADE绕点E顺时针旋转180°,设点D的像为点F.
(1)请在图中直线标出点F并连接CF;
(2)求证:四边形BCFD是平行四边形;
(3)当∠B为多少度时,四边形BCFD是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com