
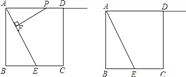
【题目】如图,正方形 ABCD 的边长为 4,E 是 BC 的中点,点 P 在射线 AD 上,过点 P 作 PF⊥AE,垂足为 F.
(1)求证:△PFA∽△ABE;
(2)当点 P 在射线 AD 上运动时,设 PA=x,是否存在实数 x,使以 P,F,E 为顶点的三角形也与△ABE
相似?若存在,求出 x 的值;若不存在,说明理由.
【答案】(1)见解析;(2)当x=2或x=5时,以P,F,E为顶点的三角形与△ABE相似.
【解析】分析:(1)在△PFA与△ABE中,易得∠PAF=∠AEB及∠PFA=∠ABE=90°;故可得△PFA∽△ABE;
(2)根据题意:若△EFP∽△ABE,则∠PEF=∠EAB;必须有PE∥AB;分两种情况进而列出关系式.
详解:证明:∵正方形ABCD
∴AD∥BC ,∠B=90°
∴∠PAF=∠AEB
∵PF⊥AE
∴∠PFA=∠B=90°
∴△PFA∽△ABE .
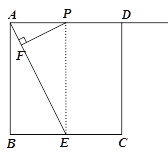
(2)情况1,当△EFP∽ABE时,则有∠PEF=∠EAB,
∴PE∥AB, ∵AD∥BC ∠B=90°
∴四边形ABEP为矩形
∴PA=EB=2,即x=2.
情况2,当△PFE∽△ABE时,且∠PEF=∠AEB时,
∵∠PAF=∠AEB
∴∠PEF=∠PAF,
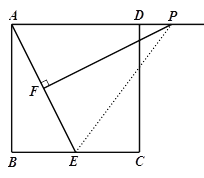
∴PE=PA
∵PF⊥AE
∴点F为AE的中点
∵AE=![]()
∴![]() ,
,
由![]() ,得:
,得:![]()
∴PE=5, ∴PA= PE=5,即x=5.
∴当x=2或x=5时,以P,F,E为顶点的三角形与△ABE相似.


科目:初中数学 来源: 题型:
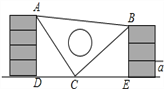
【题目】课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图.
(1)求证:△ADC≌△CEB;
(2)从三角板的刻度可知AC=25cm,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相等).
查看答案和解析>>
科目:初中数学 来源: 题型:
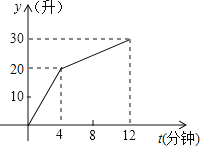
【题目】一个有进水管和一个出水管的容器,每分钟的进水量和出水量都是常数.从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水.如图表示的是容器中的水量y(升)与时间t(分钟)的图象.
(1)当4≤t≤12时,求y关于t的函数解析式;
(2)当t为何值时,y=27?
(3)求每分钟进水、出水各是多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,已知AB=CD,M、N、P分别是AD、BC、BD的中点∠ABD=20°,∠BDC=70°,则∠NMP的度数为( )

A. 50° B. 25° C. 15° D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小高从家门口骑车去离家4千米的单位上班,先花3分钟走平路1千米,再走上坡路以0.2千米/分钟的速度走了5分钟,最后走下坡路花了4分钟到达工作单位,若设他从家开始去单位的时间为t(分钟),离家的路程为y(千米),则y与t(8<t≤12)的函数关系为( )
A. y=0.5t(8<t≤12) B. y=0.5t+2(8<t≤12)
C. y=0.5t+8(8<t≤12) D. y="0." 5t-2(8<t≤12)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图象,根据图象回答下列问题:

(1)当行使8千米时,收费应为 元;
(2)从图象上你能获得哪些信息?(请写出2条)
① ________
②____________________________
(3)求出收费y(元)与行使x(千米)(x≥3)之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一段6000米的道路由甲、乙两个工程队负责完成,已知甲工程队每天完成的工作量是乙工程队每天完成工作量的2倍,且甲工程队单独完成此项工程比乙工程队单独完成此项工程少用10天.
(1)求甲、乙两工程队每天各完成多少米?
(2)如果甲工程队每天需工程费700元,乙工程队每天需工程费500元,甲工程队单独施工4天后由甲乙两个工程队共同完成余下的工程,则完成此项工程共需要多少费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC=2,∠A=∠B=30°,点D在线段AB上运动(点D不与A、B重合),连接CD,作∠CDE=30°,DE交BC于点E.
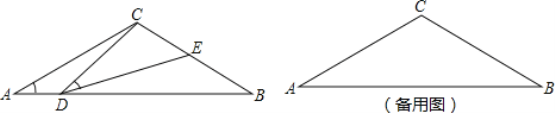
(1)AB=;
(2)当AD等于多少时,△ADC≌△BED,请说明理由;
(3)在点D的运动过程中,△CDE的形状可以是等腰三角形吗?若可以,求出AD的长;若不可以,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,□OABC的边OC在y轴的正半轴上,OC=3,A(2,1),反比例函数y=![]() (x>0)的图象经过点B.
(x>0)的图象经过点B.
(1)求点B的坐标和反比例函数的关系式;
(2)如图2,将线段OA延长交y=![]() (x>0)的图象于点D,过B,D的直线分别交x轴、y轴于E,F两点,①求直线BD的解析式;②求线段ED的长度.
(x>0)的图象于点D,过B,D的直线分别交x轴、y轴于E,F两点,①求直线BD的解析式;②求线段ED的长度.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com