
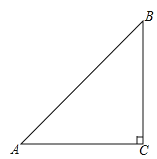
【题目】如图,已知Rt△ACB中,∠C=90°,∠BAC=45°.
(1)(4分)用尺规作图,在CA的延长线上截取AD=AB,并连接BD(不写作法,保留作图痕迹);
(2)(4分)求∠BDC的度数;
(3)(4分)定义:在直角三角形中,一个锐角A的邻边与对边的比叫做∠A的余切,记作cotA,即![]() ,根据定义,利用图形求cot22.5°的值.
,根据定义,利用图形求cot22.5°的值.
【答案】(1)答案见试题解析;(2)22.5°;(3)![]() .
.
【解析】
试题分析:(1)以点A为圆心,AB为半径作弧交CA的延长线于D,然后连结BD;
(2)由AD=AB得∠ADB=∠ABD,然后利用三角形外角性质可求出∠ADB=22.5°;
(3)设AC=x,根据题意得△ACB为等腰直角三角形,则BC=AC=x,AB=![]() ,所以AD=AB=
,所以AD=AB=![]() ,CD=
,CD=![]() ,在Rt△BCD中,根据余切的定义求解.
,在Rt△BCD中,根据余切的定义求解.
试题解析:(1)如图,

(2)∵AD=AB,∴∠ADB=∠ABD,而∠BAC=∠ADB+∠ABD,∴∠ADB=![]() ∠BAC=
∠BAC=![]() ×45°=22.5°,即∠BDC的度数为22.5°;
×45°=22.5°,即∠BDC的度数为22.5°;
(3)设AC=x,∵∠C=90°,∠BAC=45°,∴△ACB为等腰直角三角形,∴BC=AC=x,AB=![]() AC=
AC=![]() ,∴AD=AB=
,∴AD=AB=![]() ,∴CD=
,∴CD=![]() =
=![]() ,在Rt△BCD中,cot∠BDC=
,在Rt△BCD中,cot∠BDC=![]() =
=![]() =
=![]() ,即cot22.5°=
,即cot22.5°=![]() .
.


科目:初中数学 来源: 题型:
【题目】某课题小组为了解某品牌电动自行车的销售情况,对某专卖店第一季度该品牌A、B、C、D四种型号电动车的销量做了统计,绘制成如图所示的两幅统计图(均不完整) 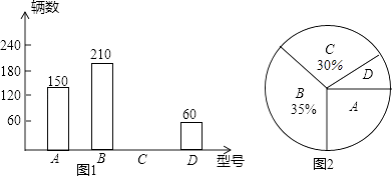
(1)该店第一季度售出这种品牌的电动自行车共多少辆?
(2)把两幅统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E,F为垂足,则下列四个结论:(1)∠DEF=∠DFE;(2)AE=AF;(3)AD平分∠EDF;(4)EF垂直平分AD.其中正确的有( ) 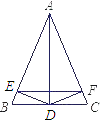
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是我们常见的地砖上的图案,其中包含了一种特殊的平面图形﹣正八边形.
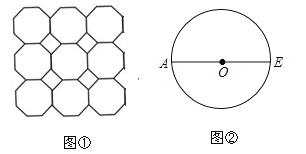
(1)如图②,AE是⊙O的直径,用直尺和圆规作⊙O的内接正八边形ABCDEFGH(不写作法,保留作图痕迹);
(2)在(1)的前提下,连接OD,已知OA=5,若扇形OAD(∠AOD<180°)是一个圆锥的侧面,则这个圆锥底面圆的半径等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动,3秒后,两点相距15个单位长度.已知动点A、B的速度比是1:4.(速度单位:单位长度/秒)
(1)求出两个动点运动的速度;
(2)若A、B两点从(1)中的位置同时向数轴负方向运动,几秒后原点恰好处在两个动点正中间;
(3)在(2)中A、B两点继续同时向数轴负方向运动时,另一动点C同时从B点位置出发向A运动,当遇到A后,立即返回向B点运动,遇到B点后立即返回向A点运动,如此往返,直到B追上A时,C立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始到停止运动,运动的路程是多少单位长度.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com