
【题目】如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD,若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( )
A. 2![]() B. 6
B. 6![]() C. 3
C. 3![]() D.
D. ![]()
![]()
【答案】C
【解析】根据矩形的性质和菱形的性质得∠ABE=∠EBD=∠DBC=30°,AB=BO=3,因为四边形BEDF是菱形,所以BE,AE可求出进而可求出BC的长.
解:∵四边形ABCD是矩形,
∴∠A=90°,
即BA⊥BF,
∵四边形BEDF是菱形,
∴EF⊥BD,∠EBO=∠DBF,
∵EF=AE+FC,AE=CF,EO=FO
∴AE=EO=CF=FO,
∴AB=BO=3,∠ABE=∠EBO,
∴∠ABE=∠EBD=∠DBC=30°,
在Rt△BAE中,设AE=x,则BE=2x,由勾股定理得,
∴AB2+AE2=BE2,即32+x2=(2x)2,
BE=2![]() ,
,
∴BF=BE=2![]() ,
,
∴CF=AE=![]() ,
,
∴BC=BF+CF=3![]() ,
,
故选C.
“点睛”本题考查了矩形的性质、菱形的性质以及在直角三角形中30°角所对的直角边时斜边的一半,解题的关键是求出∠ABE=∠EBD=∠DBC=30°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图:E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是( ) 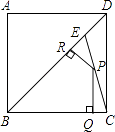
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等.经洽谈,甲商场的优惠方案是:每购买10套队服,送1个足球;乙商场的优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)每套队服和每个足球的价格分别是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所需的费用.
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的数表是由1开始的连续自然数排列而成的,根据你观察的规律完成下面问题:
(1)第8行最后一个数是________;第n行共有__________个数,这行第一个数是__________,这行最后一个数是______________.
(2)求第10行各数的和.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第一年的可变成本为2.6万元,设可变成本平均每年增长的百分率为![]()
(1)用含x的代数式表示低3年的可变成本为 万元;
(2)如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年的增长百分率x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市团委举行以“我的中国梦”为主题的知识竞赛,甲、乙两所学校的参赛人数相等,比赛结束后,发现学生成绩分别为![]() 分,
分,![]() 分,
分,![]() 分,
分,![]() 分,并根据统计数据绘制了如下不完整的统计图表:
分,并根据统计数据绘制了如下不完整的统计图表:
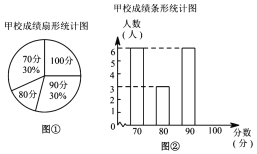
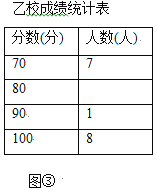
(1)乙学校的参赛人数是 人;
(2)在图①中,“![]() 分”所在扇形的圆心角度数为 ;
分”所在扇形的圆心角度数为 ;
(3)请你将图②补充完整;
(4)求乙校成绩的平均分;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com