
【题目】如图所示的数表是由1开始的连续自然数排列而成的,根据你观察的规律完成下面问题:
(1)第8行最后一个数是________;第n行共有__________个数,这行第一个数是__________,这行最后一个数是______________.
(2)求第10行各数的和.

【答案】(1)64、(2n-1)、 (n-1)2+1 、n2 ;(2)1729.
【解析】
(1)数为自然数,每行数的个数为1,3,5,…的奇数列;每行最后一个数为完全平方数,第n行最后一个数为n2.则第8行最后一个数是82;第n行共有(2n-1)个数;
第n行第一个数为(n-1)2+1;最后一个数为n2.
(2)由(1)可知第10行的第一个数是第9行最后一个数的下一个自然数,即92+1=82,最后一个数为102,求和即可.
(1) 64、(2n-1)、 (n-1)2+1 、n2
(2)82+83+84+…+98+99+100
=(82+100)+(83+99)+(84+98)+…+91
=91×2+91×2+91×2+…+91
=91×18+91
=91×19
=1729


科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明想探究函数![]() 的性质,他借助计算器求出了y与x的几组对应值,并在平面直角坐标系中画出了函数图象:
的性质,他借助计算器求出了y与x的几组对应值,并在平面直角坐标系中画出了函数图象:
x | … | -3 | -2 | -1 | 1 | 2 | 3 | … |
y | … | 2.83 | 1.73 | 0 | 0 | 1.73 | 2.83 | … |

小聪看了一眼就说:“你画的图象肯定是错误的.”
请回答:小聪判断的理由是_____________.请写出函数![]() 的一条性质:_____________.
的一条性质:_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ;将
;将![]() 沿
沿![]() 对折至
对折至![]() ,延长
,延长![]() 交边
交边![]() 于点
于点![]() ,连结
,连结![]() ,下列结论:①.
,下列结论:①.![]() ;②.
;②.![]() ;③.
;③. ![]() .其中,正确的结论有__________________.(填上你认为正确的序号)
.其中,正确的结论有__________________.(填上你认为正确的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题
(1)问题:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°,求证:ADBC=APBP;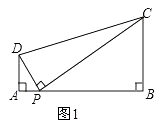
(2)探究:如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.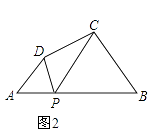
(3)应用:请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=6,AD=BD=5,点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠CPD=∠A,设点P的运动时间为t(秒),当DC=4BC时,求t的值.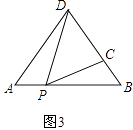
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD,若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( )
A. 2![]() B. 6
B. 6![]() C. 3
C. 3![]() D.
D. ![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下: 5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表: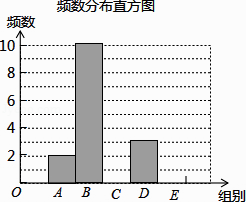
步数分组统计表
组别 | 步数分组 | 频数 |
A | 5500≤x<6500 | 2 |
B | 6500≤x<7500 | 10 |
C | 7500≤x<8500 | m |
D | 8500≤x<9500 | 3 |
E | 9500≤x<10500 | n |
请根据以上信息解答下列问题:
(1)求m,n的值;
(2)补全频数发布直方图;
(3)这20名“健步走运动”团队成员一天行走步数的中位数落在哪一组?
(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎.该打车方式的计价规则如图①所示,若车辆以平均速度vkm/h行驶了skm,则打车费用为(ps+60q·![]() )元(不足9元按9元计价).小明某天用该打车方式出行,按上述计价规则,其打车费用y(元)与行驶里程x(km)的函数关系也可由如图②表示.
)元(不足9元按9元计价).小明某天用该打车方式出行,按上述计价规则,其打车费用y(元)与行驶里程x(km)的函数关系也可由如图②表示.
(1)当x≥6时,求y与x的函数关系式.
(2)若p=1,q=0.5,求该车行驶的平均速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】武汉市光谷实验中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),下列说法错误的是( )

A. 九(1)班的学生人数为40 B. m的值为10
C. n的值为20 D. 表示“足球”的扇形的圆心角是70°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com