
【题目】已知二次函数图象的对称轴是x+3=0,图象经过(1,﹣6),且与y轴的交点为(0,![]() ).
).
(1)求这个二次函数的解析式;
(2)当x为何值时,这个函数的函数值为0;
(3)当x在什么范围内变化时,这个函数的函数值y随x的增大而增大?
【答案】(1)y=﹣![]() x2﹣3x﹣
x2﹣3x﹣ ![]() ;(2)当x为﹣1或﹣5时,这个函数的函数值为0.(3)当x<﹣3时,函数的函数值 y 随 x 的增大而增大.
;(2)当x为﹣1或﹣5时,这个函数的函数值为0.(3)当x<﹣3时,函数的函数值 y 随 x 的增大而增大.
【解析】
(1)本题实际上已知了三个条件,可设抛物线的一般形式y=ax2+bx+c求解;
(2)根据函数值为0解答;
(3)利用对称轴解答这个问题.
(1)设抛物线的解析式为y=ax2+bx+c,
由题意可得
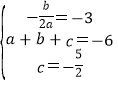 ,
,
解得a=-![]() ,b=-3,c=-
,b=-3,c=-![]() ,
,
所以y=-![]() x2-3x-
x2-3x-![]() .
.
答:这个二次函数的解析式y=-![]() x2-3x-
x2-3x-![]() .
.
(2)令y=0,得-![]() x2-3x-
x2-3x-![]() =0,
=0,
解得:x=-1或-5.
答:当x为-1或-5时,这个函数的函数值为0.
(3)由于对称轴是x=-3,开口向下,
所以当x<-3时,函数的函数值y随x的增大而增大.
答:当x<-3时,函数的函数值y随x的增大而增大.


科目:初中数学 来源: 题型:
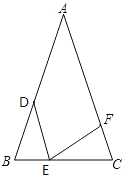
【题目】如图D、E、F分别在△ABC的三边上,BD=![]() AB,BE:EC=1:2,AC的长度是FC的3倍,四边形ADEF的面积是24,则△EFC的面积是_________.
AB,BE:EC=1:2,AC的长度是FC的3倍,四边形ADEF的面积是24,则△EFC的面积是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,AC=10,BD=6,则边长AB,AD的可能取值为( ).
A.AB=4,AD=4B.AB=4,AD=7C.AB=9,AD=2D.AB=6,AD=2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市政府于2017年初投资了112万元,建成40个公共自行车站点、配置720辆公共自行车正式启用公共自行车租贷系统:今后将逐年增加投资,用于建设新站点、配置公共自行车.预计2019年将投资340.5万元,新建120个公共自行车站点、配置2205辆公共自行车.
(1)每个站点的造价和公共自行车的单价分别是多少万元?
(2)若2017年到2019年市政府配置公共自行车数量的年平均增长率相同,请你求出2018年市政府配置公共自行车的数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一对直角三角形卡片的斜边AC重合摆放,直角顶点B,D在AC的两侧,连接BD,交AC于点O,取AC,BD的中点E,F,连接EF.若AB=12,BC=5,且AD=CD,则EF的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字2,3,4,x,甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复试验,实验数据如下表:
摸球总次数 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
“和为6”出现的频数 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
“和为6”出现的频数 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
解答下列问题:
(1)如果实验继续进行下去,根据上表数据,出现“和为6”的频率将稳定在它的概率附近,估计出现“和为6”的概率是 .
(2)当x=5时,请用列表法或树状图法计算“和为6”的概率
(3)判断x=5是否符合(1)的结论,若符合,请说明理由,若不符合,请你写出一个符合(1)的x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
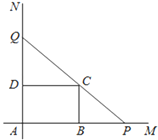
【题目】如图,互相垂直的两条公路AM、AN旁有一矩形花园ABCD,其中AB=30米,AD=20米.现欲将其扩建成一个三角形花园APQ,要求P在射线AM上,Q在射线AN上,且PQ经过点C.
(1)DQ=10米时,求△APQ的面积.
(2)当DQ的长为多少米时,△APQ的面积为1600平方米.
查看答案和解析>>
科目:初中数学 来源: 题型:
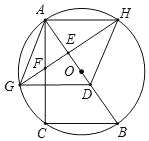
【题目】如图,Rt△ABC,CA⊥BC,AC=4,在AB边上取一点D,使AD=BC,作AD的垂直平分线,交AC边于点F,交以AB为直径的⊙O于G,H,设BC=x.
(1)求证:四边形AGDH为菱形;
(2)若EF=y,求y关于x的函数关系式;
(3)连结OF,CG.
①若△AOF为等腰三角形,求⊙O的面积;
②若BC=3,则![]() CG+9=______.(直接写出答案).
CG+9=______.(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
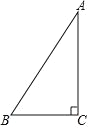
【题目】如图,△ABC 中,∠C=90°,将△ABC 绕点 C 顺时针旋转 90°,得到△DEC(其中点 D、E 分别是 A、B 两点旋转后的对应点).
(1)请画出旋转后的△DEC;
(2)试判断 DE 与 AB 的位置关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com