
【题目】如图,将一对直角三角形卡片的斜边AC重合摆放,直角顶点B,D在AC的两侧,连接BD,交AC于点O,取AC,BD的中点E,F,连接EF.若AB=12,BC=5,且AD=CD,则EF的长为_____.

【答案】![]() .
.
【解析】
先求出BE的值,作DM⊥AB,DN⊥BC延长线,先证明△ADM≌△CDN(AAS),得出AM=CN,DM=DN,再根据正方形的性质得BM=BN,设AM=CN=x,BM=AB-AM=12-x=BN=5+x,求出x=![]() ,BN=
,BN=![]() ,根据BD为正方形的对角线可得出BD=
,根据BD为正方形的对角线可得出BD=![]()
![]() , BF=
, BF=![]() BD=
BD=![]()
![]() , EF=
, EF=![]() =
=![]()
![]() .
.
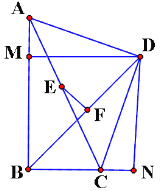
∵∠ABC=∠ADC,
∴A,B,C,D四点共圆,
∴AC为直径,
∵E为AC的中点,
∴E为此圆圆心,
∵F为弦BD中点,
∴EF⊥BD,
连接BE,∴BE=![]() AC=
AC=![]()
![]() =
=![]()
![]() =
=![]() ;
;
作DM⊥AB,DN⊥BC延长线,∠BAD=∠BCN,
在△ADM和△CDN中,
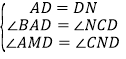 ,
,
∴△ADM≌△CDN(AAS),
∴AM=CN,DM=DN,
∵∠DMB=∠DNC=∠ABC=90°,
∴四边形BNDM为矩形,
又∵DM=DN,
∴矩形BNDM为正方形,
∴BM=BN,
设AM=CN=x,BM=AB-AM=12-x=BN=5+x,
∴12-x=5+x,x=![]() ,BN=
,BN=![]() ,
,
∵BD为正方形BNDM的对角线,
∴BD=![]() BN=
BN=![]()
![]() ,BF=
,BF=![]() BD=
BD=![]()
![]() ,
,
∴EF=![]() =
=![]() =
=![]()
![]() .
.
故答案为![]()
![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.

(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七个边长为1的正方形按如图所示的方式放置在平面直角坐标系中,直线l经过点A(4,4)和点B,且将这七个正方形的面积分成相等的两部分,则直线l的函数表达式是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是等边三角形,
是等边三角形,![]() .动点
.动点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度在边
的速度在边![]() 的延长线上运动.以
的延长线上运动.以![]() 为边作等边三角形
为边作等边三角形![]() ,点
,点![]() 在直线
在直线![]() 同侧.连结
同侧.连结![]() 相交于点
相交于点![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() .
.

(1)当![]()
![]() 时,
时,![]() .
.
(2)求证:![]() .
.
(3)求![]() 的度数.
的度数.
(4)设![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连结
,连结![]() ,当点
,当点![]() 将边
将边![]() 分成
分成![]() 的两部分时,直接写出
的两部分时,直接写出![]() 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:人教版八年级上册数学教材第121页的“阅读与思考”内容介绍,在因式分解中有一类形如x2+(p+q)x+pq的多项式,其常数项是两个因数的积,而一次项系数恰好是这两个因数的和,则我们可以把它分解成x2+(p+q)x+pq=(x+p)(x+q).
例如,x2+3x+2=x2+(1+2)x+1×2=(x+1)(x+2),具体做法是先分解二次项系数,分别写在十字交叉线的左上角和左下角,再分解常数项,分别写在十字交叉线的右上角和右下角:然后交叉相乘,求代数和,使其等于一次项系数(如图),这种方法称为“十字相乘法”.
解决问题:
(1)请模仿上例,运用十字相乘法将多项式x2﹣x﹣6因式分解(画出十字相乘图)
(2)若多项式x2+kx﹣12可以分解成(x+m)(x+n)(m,n为整数)的形式,则m+n的最大值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点D在BC上,BC平分∠ABE,BE∥AC,∠ADB=60°,∠CAD=2∠BDE,AB=14,BD=16,BE=4,则CD=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答下列问题:
神奇的等式
当a≠b时,一般来说会有a2+b≠a+b2,然而当a和b是特殊的分数时,这个等式却是成立的例如:
(![]() )2+
)2+![]() =
=![]() +
+![]() ,(
,(![]() )2+
)2+![]() =
=![]() +
+![]() ,(
,(![]() )2+
)2+![]() =
=![]() +(
+(![]() )2,…(
)2,…(![]() )2+
)2+![]() =
=![]() +(
+(![]() )2,…
)2,…
(1)特例验证:
请再写出一个具有上述特征的等式: ;
(2)猜想结论:
用n(n为正整数)表示分数的分母,上述等式可表示为: ;
(3)证明推广:
①(2)中得到的等式一定成立吗?若成立,请证明;若不成立,说明理由;
②等式(![]() )2+
)2+![]() =
=![]() +(
+(![]() )2(m,n为任意实数,且n≠0)成立吗?若成立,请写出一个这种形式的等式(要求m,n中至少有一个为无理数);若不成立,说明理由.
)2(m,n为任意实数,且n≠0)成立吗?若成立,请写出一个这种形式的等式(要求m,n中至少有一个为无理数);若不成立,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
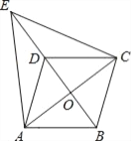
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,点E在BD的延长线上,且△EAC是等边三角形.
(1)求证:四边形ABCD是菱形.
(2)若AC=8,AB=5,求ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中, AB=11 , AC= 5 ,∠ BAC 的平分线 AD 与边 BC 的垂直平分线 DG 相 交于点 D ,过点 D 分别作 DE⊥AB ,DF⊥AC ,垂足分别为 E 、F,求BE的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com