Question

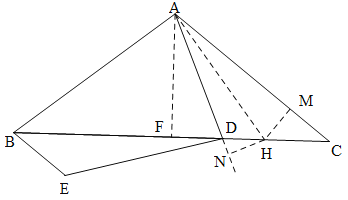
【题目】如图，△ABC中，点D在BC上，BC平分∠ABE，BE∥AC，∠ADB＝60°，∠CAD＝2∠BDE，AB＝14，BD＝16，BE＝4，则CD＝_____．

Answer 1

【答案】6．

【解析】

作AF⊥BC于BC相交于F，设FD=x，分别表示AF和BF，在Rt△ABF中根据勾股定理可解得x即FD的值（有两个），由此可求出DC，作∠DAC的平分线交DC于H,可证△EBD∽△HCA，根据相似三角形的性质可求得HC=3.5,由此可排除DC=10，所以可得DC=6.

如图：作AF⊥BC于BC相交于F，作∠DAC的平分线交DC于H,过H分别作HN⊥AN,HM⊥AC，与AN的延长线和AC分别相交于N,M.

∵BC平分∠ABE，

∴∠ABC＝∠EBC，

∵BE∥AC，

∴∠ACB＝∠EBC，

∴∠ABC＝∠ACB，

∴AB＝AC＝14，

∵AF⊥BC，

∴BF=FC，

设FD=x,

∵∠ADF=60°，BD=16，

∴AD=2x，AF，BF=16-x，DC=FC-DF=16-2x，

在Rt△ABF中根据勾股定理，

即，解得x=3或x=5，

∴DC=10或DC=6，

∵∠DAC的平分线交DC于H，∠CAD＝2∠BDE，

∴∠HAC=∠BDE，

又∵∠ABC＝∠EBC，

∴△EBD∽△HCA，

∴，即 ，解得HC=3.5，

∵∠ADF=60°，

∴∠ADC=120°，

∴AC＞AD，

∵HN⊥AN，HM⊥AC，∠DAC的平分线交DC于H，

∴HN=HM，

∴，

∴DH＜HC，

∴DC=DH+HC＜2HC＜7，

故DC=6.

答案为：6.