
【题目】如图1,△ABC中,AB=AC,∠BEF=∠DBC,∠BDC=2∠DEF,

(1)求证:BD=BE;
(2)如图2,在(1)的下,EF⊥BC,BE=8,DG=5,求CD的长;
(3)在(2)的条件下,如图3,过点C作CM⊥CB交BD的延长线于M,过点B作∠NBC=∠MBC,连接MN,且△BMN的面形为45,求BN的长.
【答案】(1)证明见解析;(2)CD=3;(3)BN=15,
【解析】
(1)证明∠BDE=∠BED,根据等角对等边得出结论;
(2)作两条垂线段,证明△BEF≌△NBD和△BGF≌△DNC,进而判断出△BFG≌△DHC即可得出CD=3,
(3)先用射影定理求出DM=![]() =
=![]() ,BM=BD+DM=
,BM=BD+DM=![]() ,CM=
,CM=![]() =
=![]() ,进而得出BH=BM=
,进而得出BH=BM=![]() ,MH=2CM=
,MH=2CM=![]() ,再用S△BMN=S△BMH+S△MNH得出NI,进而用△BCH∽△NIH,得出
,再用S△BMN=S△BMH+S△MNH得出NI,进而用△BCH∽△NIH,得出![]() ,即求出NH=
,即求出NH=![]() ,即可得出结论.
,即可得出结论.
解:(1)∵AB=AC,
∴∠C=∠ABC,
∵∠BEF=∠DBC,
∴∠EFB=∠BDC,
设∠DEF=x,∠EDB=y,∠BEF=z,
在△EGD和△BGF中,x+y=z+2x,即y=x+z,即∠BDE=∠BED,
∴BD=BE,
(2)如图2,过D作DH⊥BC,
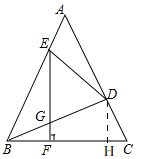
∵EF⊥BC,
∴∠BFE=∠DHB=90°
由(1)知:BE=BD,
∵∠BEF=∠DBC,∠EFB=∠DHB=90°,
∴△BEF≌△BDH(AAS),
∴BF=DH,∠EBF=∠BDH,
∵∠ABC=∠ACB,∠BEF+∠ABC=90°,.
∴∠BEF+∠ACB=90°,
∵∠BEF=∠DBC,
∴∠DBC+∠ACB=90°
∴∠BDC=90°,
∴∠BDH+∠CDH=90°,
∴∠FBG=∠HDC,
∵∠BFG=∠DHC,BF=DH,
∴△BFG≌△DHC(ASA),
∴CD=BG=BD﹣DG=3;
(3)如图3,由(2)知,CD=3,∠BDC=90°,
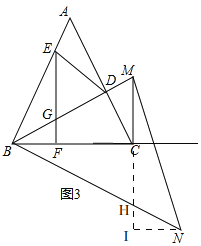
∴BC=![]() ,
,
在Rt△BCM中,CD⊥BM,
∴DM=![]() =
=![]() ,
,
∴BM=BD+DM=![]() ,CM=
,CM=![]() =
=![]() ,
,
延长MC交BN于H,
∵∠NBC=∠MBC,BC⊥MH,
∴BH=BM=![]() ,MH=2CM=
,MH=2CM=![]() ,
,
过点N作NI⊥MH交MH延长线于I,
∵△BMN的面形为45
![]() ∴NI=
∴NI=![]() ,
,
∵△BCH∽△NIH,
∴![]() ,
,
∴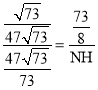 ,
,
∴NH=![]() ,
,
∴BN=BH+NH=![]() =15,
=15,


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】某校为了丰富学生的校园生活,准备购进一批篮球和足球.其中篮球的单价比足球的单价多40元,用1500元购进的篮球个数与900元购进的足球个数相等.
(1)篮球和足球的单价各是多少元?
(2)该校打算用1000元购买篮球和足球,问恰好用完1000元,并且篮球、足球都买有的购买方案有哪几种?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB,以O为圆心,以任意长为半径作弧,分别交OA,OB于F,E两点,再分别以E,F为圆心,大于![]() EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D.
EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D.
(1)若∠OFD=116°,求∠DOB的度数;
(2)若FM⊥OD,垂足为M,求证:△FMO≌△FMD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点D在BC上,BC平分∠ABE,BE∥AC,∠ADB=60°,∠CAD=2∠BDE,AB=14,BD=16,BE=4,则CD=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 轴上两点,其中
轴上两点,其中![]() 与
与![]() 互为相反数.点
互为相反数.点![]() 是第二象限内一点,且
是第二象限内一点,且![]() ,点
,点![]() 是直线
是直线![]() 上一动点;
上一动点;
(1)若![]() ,且
,且![]() 是等腰三角形,求
是等腰三角形,求![]() 的度数;
的度数;
(2)点![]() 在直线
在直线![]() 上运动过程中,当
上运动过程中,当![]() 最短时,求
最短时,求![]() 的大小.
的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
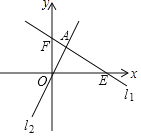
【题目】如图,在平面直角坐标系中,点E的坐标为(4,0),点F的坐标为(0,2),直线11经过点E和点F,直线l1与直线l2:y=2x相交于点A.
(1)求直线l1的表达式;
(2)求点A的坐标;
(3)求△AOE的面积;
(4)当点P是直线l1上的一个动点时,过点P作y轴的平行线PB交直线l2于点B,当线段PB=3时,请直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知矩形![]() 的边长
的边长![]() ,
,![]() ,点
,点![]() 是
是![]() 边上的一动点
边上的一动点![]() 不同于
不同于![]() 、
、![]() ,
,![]() 是
是![]() 边上的任意一点,连接
边上的任意一点,连接![]() 、
、![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,作
,作![]() 交
交![]() 于
于![]() .设
.设![]() 的长为
的长为![]() ,则
,则![]() 的面积
的面积![]() 关于
关于![]() 的函数关系式是( )
的函数关系式是( )

A. ![]() B.
B. ![]()
C. .![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com