
【题目】七个边长为1的正方形按如图所示的方式放置在平面直角坐标系中,直线l经过点A(4,4)和点B,且将这七个正方形的面积分成相等的两部分,则直线l的函数表达式是_______.

科目:初中数学 来源: 题型:
【题目】重庆市的重大惠民工程﹣﹣公租房建设已陆续竣工,计划10年内解决低收入人群的住房问题,前6年,每年竣工投入使用的公租房面积y(单位:百万平方米),与时间x的关系是y=![]() x+5,(x单位:年,1≤x≤6且x为整数);后4年,每年竣工投入使用的公租房面积y(单位:百万平方米),与时间x的关系是y=-
x+5,(x单位:年,1≤x≤6且x为整数);后4年,每年竣工投入使用的公租房面积y(单位:百万平方米),与时间x的关系是y=-![]() x+
x+![]() (x单位:年,7≤x≤10且x为整数).假设每年的公租房全部出租完.另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金z(单位:元/m2)与时间x(单位:年,1≤x≤10且x为整数)满足一次函数关系如下表:
(x单位:年,7≤x≤10且x为整数).假设每年的公租房全部出租完.另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金z(单位:元/m2)与时间x(单位:年,1≤x≤10且x为整数)满足一次函数关系如下表:
z(元/m2) | 50 | 52 | 54 | 56 | 58 | … |
x(年) | 1 | 2 | 3 | 4 | 5 | … |
(1)求出z与x的函数关系式;
(2)求政府在第几年投入的公租房收取的租金最多,最多为多少百万元;
(3)若第6年竣工投入使用的公租房可解决20万人的住房问题,政府计划在第10年投入的公租房总面积不变的情况下,要让人均住房面积比第6年人均住房面积提高a%,这样可解决住房的人数将比第6年减少1.35a%,求a的值.
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】保险公司车保险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下表:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
该公司随机调查了该险种的300名续保人在一年内的出险情况,得到如下统计图:

(1)样本中,保费高于基本保费的人数为__________名;
(2)已知该险种的基本保费a为6 000元,估计1名续保人本年度的平均保费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,BC=30cm,AC=40cm,点D在线段AB上从点B出发,以2cm/s的速度向终点A运动,设点D的运动时间为t(s).
(1)用含t的代数式表示BD的长;
(2)求AB的长;
(3)求AB边上的高;
(4)当△BCD为等腰三角形时,求t的值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学完第五章《平面直角坐标系》和第六章《一次函数》后,老师布置了这样一道思考题:已知:如图,在长方形ABCD中,BC=8,AB=4,点E为AD的中点,BD和CE相交于点P.求△BPC的面积. 小明同学应用所学知识,顺利地解决了此题,他的思路是这样的:

请你按照小明的思路解决这道思考题.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】班级组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动,基地离学校有90公里,队伍8:00从学校出发.苏老师因有事情,8:30从学校自驾小车以大巴1.5倍的速度追赶,追上大巴后继续前行,结果比队伍提前15分钟到达基地.问:
(1)大巴与小车的平均速度各是多少?
(2)苏老师追上大巴的地点到基地的路程有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一对直角三角形卡片的斜边AC重合摆放,直角顶点B,D在AC的两侧,连接BD,交AC于点O,取AC,BD的中点E,F,连接EF.若AB=12,BC=5,且AD=CD,则EF的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.
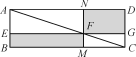
(以上材料来源于《古证复原的原则》《吴文俊与中国数学》和《古代世界数学泰斗刘徽》)
请根据上图完成这个推论的证明过程.
证明:S矩形NFGD=S△ADC-(S△ANF+S△FGC),
S矩形EBMF=S△ABC-(______________+______________).
易知,S△ADC=S△ABC,______________=______________,______________=______________.
可得S矩形NFGD=S矩形EBMF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com