
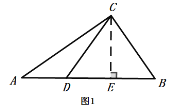
【题目】如图,Rt△ABC中,∠ACB=90°,BC=30cm,AC=40cm,点D在线段AB上从点B出发,以2cm/s的速度向终点A运动,设点D的运动时间为t(s).
(1)用含t的代数式表示BD的长;
(2)求AB的长;
(3)求AB边上的高;
(4)当△BCD为等腰三角形时,求t的值

【答案】(1)BD=2t;(2)50cm;(3)24cm;(4)当△BCD是等腰三角形时,t的值为12.5秒或15秒或18秒
【解析】
(1)先根据勾股定理求出AB,再根据点D的运动速度即可得出结论;
(2)直接利用勾股定理即可得出结论;
(3)利用直角三角形的面积S△ABC=![]() ACBC=
ACBC=![]() ABCE,建立方程求解即可得出结论;
ABCE,建立方程求解即可得出结论;
(4)分三种情况,利用等腰三角形的三线合一的性质及三角形中位线定理,即可得出结论.
(1)在Rt△ABC中,BC=30cm,AC=40cm,
根据勾股定理得,AB=![]() =
=![]() =50cm,
=50cm,
当点D运动到点A时,t=![]() =25秒,
=25秒,
∵点D的运动速度为2cm/s,
∴BD=2t(0≤t≤25);
(2)由(1)知,AB=50cm;
(3)如图1,过点C作CE⊥AB于E,
根据三角形的面积得,S△ABC=![]() ACBC=
ACBC=![]() ABCE,
ABCE,
∴CE=![]() =
=![]() =24cm,
=24cm,
即:AB边上的高为24cm;
(4)∵△BCD为等腰三角形,
∴①当BC=BD时,由(1)知,BD=2t,
∴2t=30,
∴t=15;
②当CD=CB时,如图1,过点C作CE⊥BD于E,
∴BD=2BE=2t,
∴BE=t,
∵∠BEC=∠BCA=90°,∠B=∠B,
∴△BEC∽△BCA,
∴![]() ,
,
∴BE=![]() =18,
=18,
∴t=18;
③当BD=CD时,如图2,过点D作DF⊥BC于F,
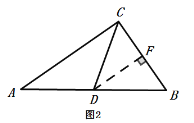
∵BD=CD,DF⊥BC
∴BF=CF,
∵∠ACB=90°,
∴∠ACB=∠BFD=90°,
∴DF∥AC,
即:DF是△ABC的中位线,
∴BD/span>=![]() AB=25,
AB=25,
∴2t=25,
∴t=12.5,
即:当△BCD是等腰三角形时,t的值为12.5秒或15秒或18秒.


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】某市为了了解2016年初中毕业生毕业后的去向,对部分九年级学生进行了抽样调查,就九年级学生的四种去向(A.读普通高中;B.读职业高中; C.直接进入社会就业; D. 其他)进行数据统计,并绘制了两幅不完整的统计图(如图① ②)请问:
(1)该市共调查了____________名初中毕业生;
(2)将两幅统计图中不完整的部分补充完整;
(3)若该市2016年九年级毕业生共有4500人,请估计该市今年九年级毕业生读普通高中的学生人数。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,圆柱底面半径为![]() ,高为
,高为![]() ,点
,点![]() 分别是圆柱两底面圆周上的点,且
分别是圆柱两底面圆周上的点,且![]() 、
、![]() 在同一母线上,用一棉线从
在同一母线上,用一棉线从![]() 顺着圆柱侧面绕3圈到
顺着圆柱侧面绕3圈到![]() ,求棉线最短为_________
,求棉线最短为_________![]() 。
。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC放置在每个小正方形边长为1的网格中,点A,B,C均在格点上,建立适当的平面直角坐标系xOy,△ABC与△A′B′C′关于y轴对称.

(1)画出该平面直角坐标系与△A′B′C′.
(2)在y轴上找点P,使PC+PB′的值最小,求点P的坐标与PC+PB'的最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试,根据测试成绩分布情况,他们将全部测试成绩分成A、B、C、D四组,绘制了如下统计图表:
“垃圾分类知识及投放情况”问卷测试成绩统计图表
组别 | 分数/分 | 频数 | 各组总分/分 |
A | 60<x≤70 | 38 | 2 581 |
B | 70<x≤80 | 72 | 5 543 |
C | 80<x≤90 | 60 | 5 100 |
D | 90<x≤100 | m | 2 796 |

依据以上统计信息,解答下列问题:
(1)求得m=________,n=__________;
(2)这次测试成绩的中位数落在______组;
(3)求本次全部测试成绩的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七个边长为1的正方形按如图所示的方式放置在平面直角坐标系中,直线l经过点A(4,4)和点B,且将这七个正方形的面积分成相等的两部分,则直线l的函数表达式是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家去李宁体育馆游泳,同时,妈妈从李宁体育馆以50米/分的速度回家,小明到体育馆后发现要下雨,立即返回,追上妈妈后,小明以250米/分的速度回家取伞,立即又以250米/分的速度折回接妈妈,并一同回家.如图是两人离家的距离y(米)与小明出发的时间x(分)之间的函数图像.(注:小明和妈妈始终在同一条笔直的公路上行走,图像上A、C、D、F四点在一条直线上)

(1)求线段oB及线段AF的函数表达式;
(2)求C点的坐标及线段BC的函数表达式;
(3)当x为 时,小明与妈妈相距1500米;
(4)求点D坐标,并说明点D的实际意义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:人教版八年级上册数学教材第121页的“阅读与思考”内容介绍,在因式分解中有一类形如x2+(p+q)x+pq的多项式,其常数项是两个因数的积,而一次项系数恰好是这两个因数的和,则我们可以把它分解成x2+(p+q)x+pq=(x+p)(x+q).
例如,x2+3x+2=x2+(1+2)x+1×2=(x+1)(x+2),具体做法是先分解二次项系数,分别写在十字交叉线的左上角和左下角,再分解常数项,分别写在十字交叉线的右上角和右下角:然后交叉相乘,求代数和,使其等于一次项系数(如图),这种方法称为“十字相乘法”.
解决问题:
(1)请模仿上例,运用十字相乘法将多项式x2﹣x﹣6因式分解(画出十字相乘图)
(2)若多项式x2+kx﹣12可以分解成(x+m)(x+n)(m,n为整数)的形式,则m+n的最大值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
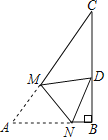
【题目】如图,已知Rt△ABC中,∠B=90°,∠A=60°,AC=2![]() +4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.
+4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com