
【题目】在平行四边形ABCD中,AC=10,BD=6,则边长AB,AD的可能取值为( ).
A.AB=4,AD=4B.AB=4,AD=7C.AB=9,AD=2D.AB=6,AD=2
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】已知点![]() ,直线
,直线![]() 无论
无论![]() 取何值,直线总过定点
取何值,直线总过定点![]() .
.
(1)求定点![]() 的坐标;
的坐标;
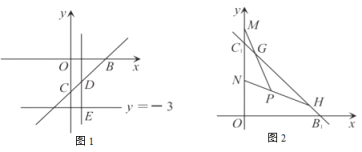
(2)如图1,若点![]() 为直线
为直线![]() 上(点
上(点![]() 除外)一动点,过点
除外)一动点,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上,距离
上,距离![]() 点为
点为![]() 个单位,
个单位,![]() 点横坐标为
点横坐标为![]() 的面积为
的面积为![]() ,求
,求![]() 与的函数关系式;
与的函数关系式;
(3)若直线![]() 关于
关于![]() 轴对称后再向上平移
轴对称后再向上平移![]() 个单位得到直线
个单位得到直线![]() ,如图2, 点
,如图2, 点![]() 和
和![]() 是直线
是直线![]() 上两点,点
上两点,点![]() 为第一象限内(
为第一象限内(![]() 两点除外)的一点,且
两点除外)的一点,且![]() ,直线
,直线![]() 和
和![]() 分别交
分别交![]() 轴于点
轴于点![]() 两点,问线段
两点,问线段![]() 有什么数量关系,并给出证明.
有什么数量关系,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
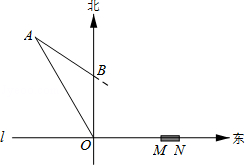
【题目】如图,在东西方向的海岸线l上有一长为1千米的码头MN,在码头西端M的正西方向30 千米处有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距![]() 千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处.
千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处.
(1)求该轮船航行的速度;
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区商店以2元的批发价进了一批纪念品.经调查发现,每个定价3元,每天可以能卖出500件,而且定价每上涨0.1元,其销售量将减少10件.根据规定:纪念品售价不能超过批发价的2.5倍.
(1)当每个纪念品定价为3.5元时,商店每天能卖出________件;
(2)如果商店要实现每天800元的销售利润,那该如何定价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形纸片 ABCD 中,∠B=∠D=90°,点 E,F 分别在边 BC,CD 上,将 AB,AD 分别沿 AE,AF 折叠,点 B,D 恰好都和点 G 重合,∠EAF=45°.
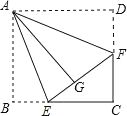
(1)求证:四边形 ABCD 是正方形;
(2)若 EC=FC=1,求 AB 的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣x2+bx+c(c>0)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3,顶点为M.
(1)求二次函数的解析式;
(2)点P为线段BM上的一个动点,过点P作x轴的垂线PQ,垂足为Q,若OQ=m,四边形ACPQ的面积为S,求S关于m的函数解析式,并写出m的取值范围;
(3)探索:线段BM上是否存在点N,使△NMC为等腰三角形?如果存在,求出点N的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数图象的对称轴是x+3=0,图象经过(1,﹣6),且与y轴的交点为(0,![]() ).
).
(1)求这个二次函数的解析式;
(2)当x为何值时,这个函数的函数值为0;
(3)当x在什么范围内变化时,这个函数的函数值y随x的增大而增大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次测绘活动中,某同学站在点A处观测停放于B、C两处的小船,测得船B在点A北偏东75°方向150米处,船C在点A南偏东15°方向120米处,则船B与船C之间的距离为______米(精确到0.1![]() ).
).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com