
【题目】已知点![]() ,直线
,直线![]() 无论
无论![]() 取何值,直线总过定点
取何值,直线总过定点![]() .
.
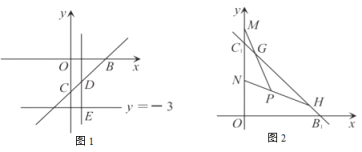
(1)求定点![]() 的坐标;
的坐标;
(2)如图1,若点![]() 为直线
为直线![]() 上(点
上(点![]() 除外)一动点,过点
除外)一动点,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上,距离
上,距离![]() 点为
点为![]() 个单位,
个单位,![]() 点横坐标为
点横坐标为![]() 的面积为
的面积为![]() ,求
,求![]() 与的函数关系式;
与的函数关系式;
(3)若直线![]() 关于
关于![]() 轴对称后再向上平移
轴对称后再向上平移![]() 个单位得到直线
个单位得到直线![]() ,如图2, 点
,如图2, 点![]() 和
和![]() 是直线
是直线![]() 上两点,点
上两点,点![]() 为第一象限内(
为第一象限内(![]() 两点除外)的一点,且
两点除外)的一点,且![]() ,直线
,直线![]() 和
和![]() 分别交
分别交![]() 轴于点
轴于点![]() 两点,问线段
两点,问线段![]() 有什么数量关系,并给出证明.
有什么数量关系,并给出证明.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,![]() 的三个顶点在坐标轴上,
的三个顶点在坐标轴上,![]() ,且
,且![]() ,将
,将![]() 沿着
沿着![]() 翻折到
翻折到![]() .
.

(1)求点![]() 的坐标;
的坐标;
(2)动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 轴以
轴以![]() 个单位秒的速度向终点
个单位秒的速度向终点![]() 运动,过点
运动,过点![]() 作直线
作直线![]() 垂直于
垂直于![]() 轴,分别交直线
轴,分别交直线![]() 、直线
、直线![]() 于点
于点![]() 、
、![]() ,设线段
,设线段![]() 的长为
的长为![]() ,点
,点![]() 运动时间为
运动时间为![]() 秒,求
秒,求![]() 与
与![]() 的关系式,并写出
的关系式,并写出![]() 的取值范围.
的取值范围.
(3如图2在(2)的条件下,点![]() 为点
为点![]() 关于
关于![]() 轴的对称点,点
轴的对称点,点![]() 在直线
在直线![]() 上,是否存在点
上,是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形;若存在,求出
为顶点的四边形为平行四边形;若存在,求出![]() 值和点
值和点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次男子马拉松长跑比赛中,随机抽得12名选手所用的时间(单位:分钟)得到如下样本数据:140 146 143 175 125 164 134 155 152 168 162 148
(1)计算该样本数据的中位数和平均数;
(2)如果一名选手的成绩是147分钟,请你依据样本数据的中位数,推断他的成绩如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,以BC为直径的⊙O与AD相切,点E为AD的中点,下列结论正确的个数是( )
(1)AB+CD=AD;(2)S△BCE=S△ABE+S△DCE;(3)ABCD=![]() ;(4)∠ABE=∠DCE.
;(4)∠ABE=∠DCE.
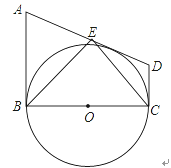
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请根据统计图中所提供的信息解答下列问题:
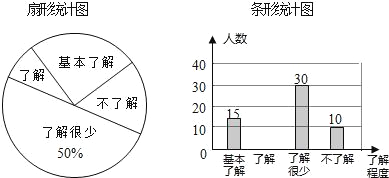
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 度;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 的顶点
的顶点![]() 分别在
分别在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在反比例函数
在反比例函数![]() 的第一象限内的图像上,
的第一象限内的图像上,![]() ,动点
,动点![]() 在
在![]() 轴的上方,且满足
轴的上方,且满足![]() .
.
(1)若点![]() 在这个反比例函数的图像上,求点
在这个反比例函数的图像上,求点![]() 的坐标;
的坐标;
(2)连接![]() ,求
,求![]() 的最小值;
的最小值;
(3)若点![]() 是平面内一点,使得以
是平面内一点,使得以![]() 为顶点的四边形是菱形,则请你直接写出满足条件的所有点
为顶点的四边形是菱形,则请你直接写出满足条件的所有点![]() 的坐标.
的坐标.
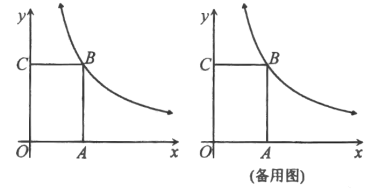
查看答案和解析>>
科目:初中数学 来源: 题型:
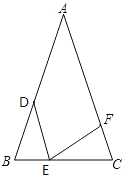
【题目】如图D、E、F分别在△ABC的三边上,BD=![]() AB,BE:EC=1:2,AC的长度是FC的3倍,四边形ADEF的面积是24,则△EFC的面积是_________.
AB,BE:EC=1:2,AC的长度是FC的3倍,四边形ADEF的面积是24,则△EFC的面积是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,AC=10,BD=6,则边长AB,AD的可能取值为( ).
A.AB=4,AD=4B.AB=4,AD=7C.AB=9,AD=2D.AB=6,AD=2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com