
【题目】如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,以BC为直径的⊙O与AD相切,点E为AD的中点,下列结论正确的个数是( )
(1)AB+CD=AD;(2)S△BCE=S△ABE+S△DCE;(3)ABCD=![]() ;(4)∠ABE=∠DCE.
;(4)∠ABE=∠DCE.
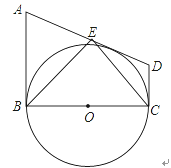
A. 1 B. 2 C. 3 D. 4
【答案】D
【解析】
设AD和半圆O相切的切点为F,连接OF,根据切线长定理以及相似三角形的判定和性质逐项分析即可.
设AD和半圆O相切的切点为F,
∵在直角梯形ABCD中AB∥CD,AB⊥BC,
∴![]()
∵AB为直径,
∴AB,CD是圆的切线,
∵AD与以AB为直径的⊙O相切,
∴AB=AF,CD=DF,
∴AD=AF+DF=AB+CD,故①正确;
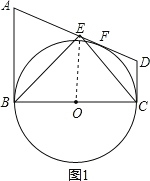
如图1,连接OE,
∵AE=DE,BO=CO,
∴OE∥AB∥CD,OE=![]() (AB+CD),
(AB+CD),
∴OE⊥BC,
 故②正确;
故②正确;
如图2,连接AO,OD,
∵AB∥CD,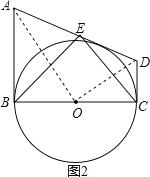
∴![]()
∵AB,CD,AD是O的切线,
∴![]()
∴![]()
∴![]()
∴∠BAO=∠DOC,
∴△ABO∽△OCD,
∴![]()
∴![]() ,故③正确,
,故③正确,
如图1,∵OB=OC,OE⊥BC,
∴BE=CE,
∴∠BEO=∠CEO,
∵AB∥OE∥CD,
∴∠ABE=∠BEO,∠DCE=∠OEC,
∴∠ABE=∠DCE,故④正确,
综上可知正确的个数有4个,
故选:D.


科目:初中数学 来源: 题型:
【题目】![]() 是一张等腰直角三角形纸板,
是一张等腰直角三角形纸板,![]() ,
,![]() ,在这张纸板中剪出一个尽可能大的正方形称为第
,在这张纸板中剪出一个尽可能大的正方形称为第![]() 次剪取;在余下的
次剪取;在余下的![]() 和
和![]() 中,分别剪取正方形,得到两个相同的正方形,称为第
中,分别剪取正方形,得到两个相同的正方形,称为第![]() 次剪取(如图
次剪取(如图![]() );继续操作下去…;第
);继续操作下去…;第![]() 次剪取后,余下的所有小三角形的面积之和是________.
次剪取后,余下的所有小三角形的面积之和是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
(3)若AD=3,AE=5,则菱形AECF的面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A、B、C是直径为6cm的⊙O上的点,且AB=3cm,AC=3![]() cm,则∠BAC的度数为( )
cm,则∠BAC的度数为( )
A. 15° B. 75°或15° C. 105°或15° D. 75°或105°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC内接于⊙O,AC是⊙O的直径,D是![]() 的中点.过点D作CB的垂线,分别交CB、CA延长线于点F、E.
的中点.过点D作CB的垂线,分别交CB、CA延长线于点F、E. 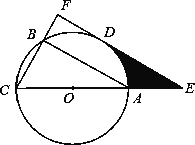
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若CF=6,∠ACB=60°,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,BC切⊙O于点B,AD⊥BC,垂足为D,OA是⊙O的半径,且OA=3.
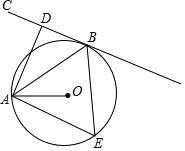
(1)求证:AB平分∠OAD;
(2)若点E是优弧 ![]() 上一点,且∠AEB=60°,求扇形OAB的面积.(计算结果保留π)
上一点,且∠AEB=60°,求扇形OAB的面积.(计算结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
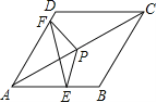
【题目】如图,把△EFP按图示方式放置在菱形ABCD中,使得顶点E、F、P分别在线段AB、AD、AC上,已知EP=FP=4,EF=4![]() ,∠BAD=60°,且AB>4
,∠BAD=60°,且AB>4![]() .
.
(1)求∠EPF的大小;
(2)若AP=6,求AE+AF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com