
【题目】![]() 是一张等腰直角三角形纸板,
是一张等腰直角三角形纸板,![]() ,
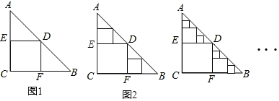
,![]() ,在这张纸板中剪出一个尽可能大的正方形称为第
,在这张纸板中剪出一个尽可能大的正方形称为第![]() 次剪取;在余下的
次剪取;在余下的![]() 和
和![]() 中,分别剪取正方形,得到两个相同的正方形,称为第
中,分别剪取正方形,得到两个相同的正方形,称为第![]() 次剪取(如图
次剪取(如图![]() );继续操作下去…;第
);继续操作下去…;第![]() 次剪取后,余下的所有小三角形的面积之和是________.
次剪取后,余下的所有小三角形的面积之和是________.
【答案】![]()
【解析】
根据题意,可求得S△AED+S△DBF=S正方形ECFD=S1=4,同理可得规律:Sn即是第n次剪取后剩余三角形面积和,根据此规律求解即可答案.
∵四边形ECFD是正方形,
∴DE=EC=CF=DF,∠AED=∠DFB=90°,
∵△ABC是等腰直角三角形,
∴∠A=∠B=45°,
∴AE=DE=EC=DF=BF=EC=CF,
∵AC=BC=4,
∴DE=DF=2,
∴S△AED+S△DBF=S正方形ECFD=S1=4,
同理:S2即是第二次剪取后剩余三角形面积和,Sn即是第n次剪取后剩余三角形面积和,
∴第一次剪取后剩余三角形面积和为:8-S1=4=22=S1,
第二次剪取后剩余三角形面积和为:S1-S2=4-2=21=S2,
第三次剪取后剩余三角形面积和为:S2-S3=20=S3,
…
第n次剪取后剩余三角形面积和为:Sn-1-Sn=Sn=![]() ,
,
故第64次剪取后,余下的所有小三角形的面积之和是:![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
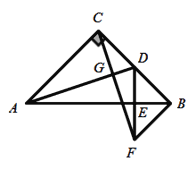
【题目】如图,在等腰![]() 中,
中,![]() ,D为BC的中点,过点C作
,D为BC的中点,过点C作![]() 于点G,过点B作
于点G,过点B作![]() 于点B,交CG的延长线于点F,连接DF交AB于点E.
于点B,交CG的延长线于点F,连接DF交AB于点E.
(1)求证:![]() ;
;
(2)求证:AB垂直平分DF;
(3)连接AF,试判断![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某仓储中心有一斜坡AB,其坡比为i=1∶2,顶部A处的高AC为4 m,B,C在同一水平面上.
(1)求斜坡AB的水平宽度BC;
(2)矩形DEFG为长方形货柜的侧面图,其中DE=2.5 m,EF=2 m.将货柜沿斜坡向上运送,当BF=3.5 m时,求点D离地面的高.(![]() ≈2.236,结果精确到0.1 m)
≈2.236,结果精确到0.1 m)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形,∠BAC= 90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.

(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3![]() 时,求线段DH的长.
时,求线段DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC 中,AB、AC 边的垂直平分线相交于点 O,分别交 BC 边于点 M、N,连接 AM,AN.

(1)若△AMN 的周长为 6,求 BC 的长;
(2)若∠MON=30°,求∠MAN 的度数;
(3)若∠MON=45°,BM=3,BC=12,求 MN 的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是边长为1的正方形ABCD的对角线,BE平分∠DBC交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G.
(1)求证:△BCE≌△DCF;
(2)求CF的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
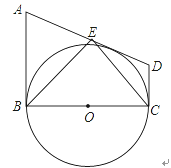
【题目】如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,以BC为直径的⊙O与AD相切,点E为AD的中点,下列结论正确的个数是( )
(1)AB+CD=AD;(2)S△BCE=S△ABE+S△DCE;(3)ABCD=![]() ;(4)∠ABE=∠DCE.
;(4)∠ABE=∠DCE.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com