
【题目】如图在△ABC 中,AB、AC 边的垂直平分线相交于点 O,分别交 BC 边于点 M、N,连接 AM,AN.

(1)若△AMN 的周长为 6,求 BC 的长;
(2)若∠MON=30°,求∠MAN 的度数;
(3)若∠MON=45°,BM=3,BC=12,求 MN 的长度.
【答案】(1)6;(2)120°(3)5.
【解析】
(1)根据垂直平分线的性质可得BM=AM,CN=AN,再根据三角形的周长即可求出BC;
(2)设射线OM交AB于E,射线ON交AC于F,根据四边形的内角和,即可求出∠EAF,再根据三角形的内角和,即可求出∠B+∠C,然后根据等边对等角即可求出∠MAB+∠NAC,从而求出∠MAN;
(3)设射线OM交AB于E,射线ON交AC于F,根据四边形的内角和,即可求出∠EAF,再根据三角形的内角和,即可求出∠B+∠C,然后根据等边对等角即可求出∠MAB+∠NAC,从而求出∠MAN,设MN=x,根据勾股定理列出方程求出x即可.
解:(1)∵AB、AC 边的垂直平分线相交于点 O,分别交 BC 边于点 M、N,
∴BM=AM,CN=AN
∵△AMN 的周长为 6,
∴AM+AN+MN=6
∴BC=BM+MN+CN= AM+MN+AN =6;
(2)设射线OM交AB于E,射线ON交AC于F,
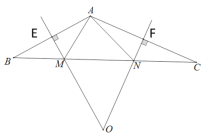
在四边形AEOF中,∠EAF=360°-∠AEO-∠AFO-∠MON=150°
∴∠B+∠C=180°-∠BAC=30°
∵BM=AM,CN=AN
∴∠MAB=∠B,∠NAC=∠C
∴∠MAB+∠NAC=30°
∴∠MAN=∠EAF-(∠MAB+∠NAC)=120°;
(3)设射线OM交AB于E,射线ON交AC于F,

在四边形AEOF中,∠EAF=360°-∠AEO-∠AFO-∠MON=135°
∴∠B+∠C=180°-∠BAC=45°
∵BM=AM=3,CN=AN
∴∠MAB=∠B,∠NAC=∠C
∴∠MAB+∠NAC=45°
∴∠MAN=∠EAF-(∠MAB+∠NAC)=90°
设MN=x,则AN =CN=BC-BM-MN=9-x
在Rt△AMN中,MN2=AM2+AN2
即x2=32+(9-x)2
解得:x=5
即MN=5


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
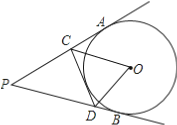
【题目】如图,P为⊙O外一点,PA,PB分别切⊙O于A,B,CD切⊙O于点E,分别交PA,PB于点C,D.若PA=5,则△PCD的周长和∠COD分别为( )
A. 5, ![]() (90°+∠P) B. 7,90°+
(90°+∠P) B. 7,90°+![]() C. 10,90°-
C. 10,90°-![]() ∠P D. 10,90°+
∠P D. 10,90°+![]() ∠P
∠P
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,并回答下列问题:
小明遇到这样一个问题,如图,在![]() 中,
中,![]() 分别交
分别交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .已知
.已知![]() ,求
,求![]() 的值.
的值.
小明发现,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,构造
,构造![]() ,经过推理和计算能够使问题得到解决(如图)
,经过推理和计算能够使问题得到解决(如图)

请你回答:
(1)证明:![]() ;
;
(2)求出![]() 的值;
的值;
(3)参考小明思考问题的方法,解决问题;
如图,已知![]() 和矩形
和矩形![]() 与
与![]() 交于点
交于点![]() .求
.求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为一幅重叠放置的三角板,其中∠ABC=∠EDF=90°,BC与DF共线,将△DEF沿CB方向平移,当EF经过AC的中点O时,直线EF交AB于点G,若BC=3,则此时OG的长度为( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的外接圆为⊙O,点P在劣弧 CD上(不与C点重合).
(1)求∠BPC的度数;
(2)若⊙O的半径为8,求正方形ABCD的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
(1)作出△ABC关于原点O成中心对称的△A1B1C1;
(2)直接写出:以A、B、C为顶点的平形四边形的第四个顶点D的坐标 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上,点O为原点,点A表示的数为9,动点B,C在数轴上移动,且总保持BC=2(点C在点B右侧),设点B表示的数为m.
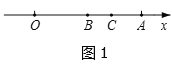

(1) 如图1,当B,C在线段OA上移动时,
① 若B为OA中点,则AC= ;
② 若B,C移动到某一位置时,恰好满足AC=OB,求此时m的值;
(2) 当线段BC沿射线AO方向移动时,若存在AC-OB=![]() AB,求满足条件的m值.
AB,求满足条件的m值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com