
【题目】如图,为一幅重叠放置的三角板,其中∠ABC=∠EDF=90°,BC与DF共线,将△DEF沿CB方向平移,当EF经过AC的中点O时,直线EF交AB于点G,若BC=3,则此时OG的长度为( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在 13×7 的网格中,每个小正方形边长都是 1,其顶点叫做格点,如图 A、B、D、E 均为格点,![]() ABD 为格点三角形.
ABD 为格点三角形.

(1)请在给定的网格中画 ABCD,要求 C 点在格点上;
(2)在(1)中 ABCD 右侧,以格点 E 为其中的一个顶点,画格点![]() EFG,并使 EF=5,FG=3,EG=
EFG,并使 EF=5,FG=3,EG=![]()
(3)先将(2)中的线段 EF 向右平移 6 个单位、再向下平移 l 个单位到 MP 的位置,再以 MP 为对角线画矩形 MNPQ(M、N、P、Q 按逆时针方向排列),直接写出矩形 MNPQ 的面积为 ______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,E是CB延长线上一个动点,F、G分别为AE、BC的中点,FG与ED相交于点H.
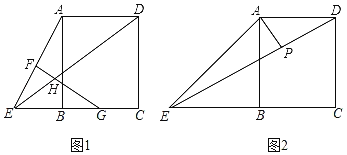
(1)求证:HE=HG;
(2)如图2,当BE=AB时,过点A作AP⊥DE于点P,连接BP,求![]() 的值;
的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】六(2)班同学准备春游,某品牌牛奶每盒200毫升,售价2元.
(1)在甲商店购买,买5盒送一盒;在乙商场购买,九折优惠.全班42人,要给每位同学准备一瓶这样的牛奶,该去哪家商场购买比较合算?为什么?
(2)商店提供装牛奶的是一个长方体纸箱,下面是它的展开图,请算出这个长方体纸箱的表面积.(黏贴处不算,单位:分米)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,以点B为圆心,任意长为半径画弧,分别交AB、BC于点M、N分别以点M、N为圆心,以大于![]() MN的长度为半径画弧两弧相交于点P过点P作线段BD,交AC于点D,过点D作DE⊥AB于点E,则下列结论①CD=ED;②∠ABD=
MN的长度为半径画弧两弧相交于点P过点P作线段BD,交AC于点D,过点D作DE⊥AB于点E,则下列结论①CD=ED;②∠ABD=![]() ∠ABC;③BC=BE;④AE=BE中,一定正确的是( )
∠ABC;③BC=BE;④AE=BE中,一定正确的是( )
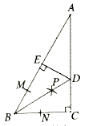
A. ①②③B. ① ② ④C. ①③④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC 中,AB、AC 边的垂直平分线相交于点 O,分别交 BC 边于点 M、N,连接 AM,AN.

(1)若△AMN 的周长为 6,求 BC 的长;
(2)若∠MON=30°,求∠MAN 的度数;
(3)若∠MON=45°,BM=3,BC=12,求 MN 的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OABC是平行四边形,对角线OB在轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=![]() 和y=
和y=![]() 的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①
的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①![]() ;②阴影部分面积是
;②阴影部分面积是![]() (k1+k2);③当∠AOC=90°时,|k1|=|k2|;④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是( )
(k1+k2);③当∠AOC=90°时,|k1|=|k2|;④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是( )

A.①②B.①④C.③④D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AD平分∠BAC交⊙O于点D,过点D作DE∥BC交AC的延长线于点E.

(1)试判断DE与⊙O的位置关系,并证明你的结论;
(2)若∠E=60°,⊙O的半径为5,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() 的图象如图,有以下结论:
的图象如图,有以下结论:
①m<0;
②在每一个分支上,y随x的增大而增大;
③若点A(-1,a)、B(2,b)在图象上,则a<b;
④若点P(x,y)在图象上,则点P1(-x,-y)也在图象上.
其中正确结论的个数为( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com