
【题目】如图1,在矩形ABCD中,E是CB延长线上一个动点,F、G分别为AE、BC的中点,FG与ED相交于点H.
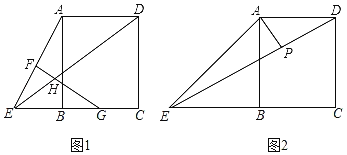
(1)求证:HE=HG;
(2)如图2,当BE=AB时,过点A作AP⊥DE于点P,连接BP,求![]() 的值;
的值;
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接AG,并延长AG交DC的延长线于M,连接EM,证明先证明△ABG≌△MCG(ASA),得到GA=GM,加上已知F为AE的中点,进而证明FG是△AEM的中位线,根据中位线的性质可得∠HGE=∠MEC,接下来用SAS证明△DEC≌△MEC,可得∠DEC=∠MEC,所以∠HEG=∠HGE,HE=HG即得以证明;
(2)过点B作BQ⊥BP交DE于Q,在△ABP和△EBQ中,根据三角形内角和定理及对顶角相等的性质,易得∠BEQ=∠BAP,由∠QBP=∠ABE=90°可得∠QBP=∠ABE=90°,又因为BE=AB,所以满足ASA,△BEQ≌△BAP可证;再根据全等三角形的性质可得BQ=BP,PA=QE,可证△PBQ是等腰直角三角形,![]() ,而PQ=
,而PQ=![]() PB,等量代换代入所求比例式,即可求解.
PB,等量代换代入所求比例式,即可求解.
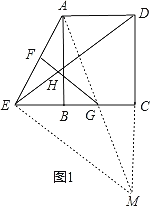
(1)证明:连接AG,并延长AG交DC的延长线于M,连接EM,
 ,
,
∵G为BC的中点,
∴BG=CG,
∵四边形ABCD是矩形,
∴∠ABG=∠DCB=90°,
∴∠ABG=∠MCG=90°,
在△ABG和△MCG中,
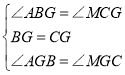 ,
,
∴△ABG≌△MCG(ASA),
∴GA=GM,
∵F为AE的中点,
∴FA=FE,
∴FG是△AEM的中位线,
∴FG∥EM,
∴∠HGE=∠MEC,
在△DCE和△MCE中,
![]()
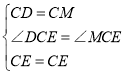 ,
,
∴△DEC≌△MEC(SAS),
∴∠DEC=∠MEC,
∵∠HGE=∠MEC,
∴∠HEG=∠HGE,
∴HE=HG;
(2)过点B作BQ⊥BP交DE于Q,则∠QBP=90°,
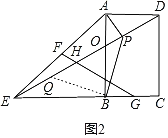
∵AP⊥DE,四边形ABCD是矩形,
∴∠APE=∠ABE=90°,
∵∠APO+∠AOP+∠BAP=180°,∠EOB+∠ABE+∠BEP=180°,∠AOP=∠EOB,
∴∠BEQ=∠BAP,
∵∠QBP=∠ABE=90°,
∴∠EBQ=∠ABP=90°﹣∠ABQ,
在△ABP和△EBQ中,
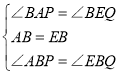 ,
,
∴△BEQ≌△BAP(ASA),
∴BQ=BP,PA=QE,
∴△PBQ是等腰直角三角形,
∴PQ=![]() PB,
PB,
∴![]() .
.


科目:初中数学 来源: 题型:
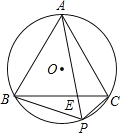
【题目】如图,正![]() 内接于
内接于![]() 是劣弧BC上任意一点,PA与BC交于点E,有如下结论:
是劣弧BC上任意一点,PA与BC交于点E,有如下结论:
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() 图中共有6对相似三角形.
图中共有6对相似三角形.
其中,正确结论的个数为![]()
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,
(1)写出数轴上点B表示的数 ;
(2)|5﹣3|表示5与3之差的绝对值,实际上也可理解为5与3两数在数轴上所对的两点之间的距离.如|x﹣3|的几何意义是数轴上表示有理数x的点与表示有理数3的点之间的距离.试探索:
①:若|x﹣8|=2,则x= .
②:|x+12|+|x﹣8|的最小值为 .
(3)动点P从O点出发,以每秒5个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.求当t为多少秒时?A,P两点之间的距离为2;
(4)动点P,Q分别从O,B两点,同时出发,点P以每秒5个单位长度沿数轴向右匀速运动,Q点以P点速度的两倍,沿数轴向右匀速运动,设运动时间为t(t>0)秒.问当t为多少秒时?P,Q之间的距离为4.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有30箱苹果,以每箱20千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质质量的差 (单位:千克) |
|
|
| 1 | 2 |
箱数 | 2 | 6 | 10 | 8 | 4 |
(1)这30箱苹果中,最重的一箱比最轻的一箱重多少千克?
(2)与标准质量比较,这30箱苹果总计超过或不足多少千克?
(3)若苹果每千克售价6元,则出售这30箱苹果可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为一幅重叠放置的三角板,其中∠ABC=∠EDF=90°,BC与DF共线,将△DEF沿CB方向平移,当EF经过AC的中点O时,直线EF交AB于点G,若BC=3,则此时OG的长度为( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com